题目内容
设p:9x-4•3x+1+27=0,q:log2(x+1)+log2x=log26,则p是q的
- A.充分不必要条件
- B.必要不充分条件
- C.充分且必要条件
- D.既不充分也不必要条件
B
分析:先求出指数方程的解得到p,然后解对数方程的解得到q,根据小范围推大范围可得p与q的关系.
解答:∵p:9x-4•3x+1+27=0
∴p:(3x-3)(3x-9)=0解得x=1或2
∵q:log2(x+1)+log2x=log26
∴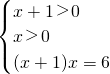 解得x=2
解得x=2
∵p不能推q,q能推p
∴p是q的必要不充分条件
故选B.
点评:本题主要考查了指数方程的解法和对数方程的解法,以及必要条件、充分条件与充要条件的判断,同时考查了运算求解的能力,属于基础题.
分析:先求出指数方程的解得到p,然后解对数方程的解得到q,根据小范围推大范围可得p与q的关系.
解答:∵p:9x-4•3x+1+27=0
∴p:(3x-3)(3x-9)=0解得x=1或2
∵q:log2(x+1)+log2x=log26
∴
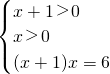 解得x=2
解得x=2∵p不能推q,q能推p
∴p是q的必要不充分条件
故选B.
点评:本题主要考查了指数方程的解法和对数方程的解法,以及必要条件、充分条件与充要条件的判断,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目