Question

22、某城市数、理、化竞赛时，高一某班有24名学生参加数学竞赛，28名学生参加物理竞赛，19名学生参加化学竞赛，其中参加数、理、化三科竞赛的有7名，只参加数、物两科的有5名，只参加物、化两科的有3名，只参加数、化两科的有4名．若该班学生共有48名，问没有参加任何一科竞赛的学生有多少名？

Answer 1

分析：首先分析题目，发现题目已知条件太多，考虑到画图使条件简化，然后根据图形求出单独参加数理化的人数，然后把单独参加数理化的人数和参加2门参加3门竞赛的人数加在一起，即可得到参加竞赛的人数，拿总人数减去它即可得到答案．

解答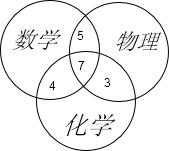：解：画三个圆分别代表参加数学、物理、化学的人．
因为参加数、理、化三科竞赛的有7名，
只参加数、物两科的有5名，
只参加物、化两科的有3名，
只参加数．化两科的有4名．
分别填入图形中
又因为有24名学生参加数学竞赛，28名学生参加物理竞赛，19名学生参加化学竞赛．
故单独参加数学的有8人、单独参加物理的有13人，单独参加化学的有5人，
故8+13+5+5+7+4+3=45是参加竞赛的人数，所以没参加的人数为48-45=3人．
故答案为3．

点评：此题主要考查数形结合思想在解决实际问题中的应用，题目已知条件过多，技巧性较强．同学们做此类题目要注意选择合适的解题方法．