题目内容
已知关于x，y的方程C：x2+y2-2x-4y+m=0．
（1）当m为何值时，方程C表示圆．
（2）若圆C与直线l：x+2y-4=0相交于M，N两点，且MN=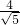
，求m的值．
解：（1）方程C可化为：（x-1）2+（y-2）2=5-m，显然，当5-m＞0时，即m＜5时，方程C表示圆．
（2）圆的方程化为（x-1）2+（y-2）2=5-m，圆心C（1，2），半径
，
则圆心C（1，2）到直线l：x+2y-4=0 的距离为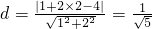
，
∵
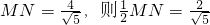，有 
，
∴
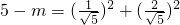，解得 m=4．
分析：（1）方程C可化为：（x-1）2+（y-2）2=5-m，应有5-m＞0．
（2）先求出圆心坐标和半径，圆心到直线的距离，利用弦长公式求出m的值．
点评：本题考查圆的标准方程的特征，点到直线的距离公式、弦长公式的应用．
（2）圆的方程化为（x-1）2+（y-2）2=5-m，圆心C（1，2），半径
，则圆心C（1，2）到直线l：x+2y-4=0 的距离为
，∵
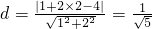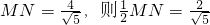，有 ，∴
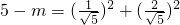，解得 m=4．分析：（1）方程C可化为：（x-1）2+（y-2）2=5-m，应有5-m＞0．
（2）先求出圆心坐标和半径，圆心到直线的距离，利用弦长公式求出m的值．
点评：本题考查圆的标准方程的特征，点到直线的距离公式、弦长公式的应用．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目