题目内容
已知点O是△ABC内的一点，∠AOB=150°，∠BOC=90°，
=
，
=
，
=
，|
|=2，|
|=1，|
|=3．
（1）设实数t满足（
-t
）•
=0，求t的值；
（2）试用
，
表示
．
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
（1）设实数t满足（
| AB |
| OC |
| OC |
（2）试用
| a |
| b |
| c |
（1）∵（
-t
）•
=0，
∴（
-
-t
）•
=0
∵∠AOB=150°，∠BOC=90°
∴∠AOC=120°，
∵
=
，
=
，
=
，|
|=2，|
|=1，|
|=3
∴-3-9t=0
∴t=
；
（2）设
=m
+n
，则
•
=m
•
+n
•
，
•
=m
•
+n
2
∴
∴m=-3，n=3
∴
=-3
+3
．
| AB |
| OC |
| OC |
∴（
| OB |
| OA |
| OC |
| OC |
∵∠AOB=150°，∠BOC=90°
∴∠AOC=120°，
∵
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
∴-3-9t=0
∴t=
| 1 |
| 3 |
（2）设
| c |
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| c |
| c |
| b |
| a |
| b |
| b |
∴
|
∴m=-3，n=3
| 3 |
∴
| c |
| a |
| 3 |
| b |
练习册系列答案
黄冈冠军课课练系列答案
相关题目
，OC=c，且|a|=2，|b|=1，|c|=3，试用a、b表示c．
，OC=c，且|a|=2，|b|=1，|c|=3，试用a、b表示c．
=
，
=
，
=
，|
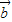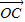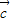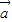|=2，|
|=1，|
|=3．
-t
）•
=0，求t的值；
，
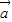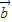表示
．