题目内容
已知抛物线 与双曲线
与双曲线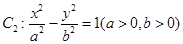 有公共焦点
有公共焦点 ,点
,点 是曲线
是曲线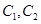 在第一象限的交点,且
在第一象限的交点,且 .
.
(1)求双曲线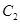 的方程;
的方程;
(2)以双曲线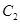 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆 与直线
与直线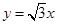 相切,圆
相切,圆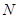 :
: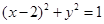 .过点
.过点 作互相垂直且分别与圆
作互相垂直且分别与圆 、圆
、圆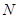 相交的直线
相交的直线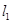 和
和 ,设
,设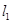 被圆
被圆 截得的弦长为
截得的弦长为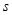 ,
, 被圆
被圆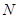 截得的弦长为
截得的弦长为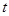 ,问:
,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】
(1) 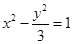 ;(2)
;(2)
 .
.
【解析】
试题分析:(1)由抛物线的焦点求的双曲线的焦点坐标,再由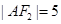 求得
求得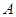 点坐标,再结合双曲线的定义可得双曲线的方程;(2)首先利用直线与圆相切求得圆
点坐标,再结合双曲线的定义可得双曲线的方程;(2)首先利用直线与圆相切求得圆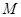 ,再利用弦长公式求弦长,化简求值即可,需注意直线的形式,有无斜率需考虑.
,再利用弦长公式求弦长,化简求值即可,需注意直线的形式,有无斜率需考虑.
试题解析:(1)∵抛物线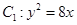 的焦点为
的焦点为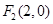 ,
,
∴双曲线 的焦点为
的焦点为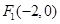 、
、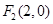 ,
1分
,
1分
设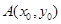 在抛物线
在抛物线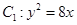 上,且
上,且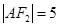 ,
,
由抛物线的定义得,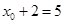 ,∴
,∴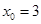 ,∴
,∴ ,∴
,∴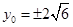 ,
3分
,
3分
∴ ,
4分
,
4分
又∵点 在双曲线
在双曲线 上,由双曲线定义得:
上,由双曲线定义得:
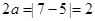 ,∴
,∴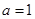 ,
∴双曲线
,
∴双曲线 的方程为:
的方程为: .
6分
.
6分
(2)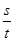 为定值.下面给出说明.
为定值.下面给出说明.
设圆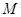 的方程为:
的方程为: ,
∵圆
,
∵圆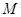 与直线
与直线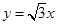 相切,
相切,
∴圆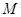 的半径为
的半径为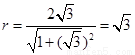 ,故圆
,故圆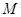 :
: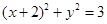 .
7分
.
7分
显然当直线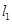 的斜率不存在时不符合题意,
8分
的斜率不存在时不符合题意,
8分
设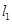 的方程为
的方程为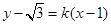 ,即
,即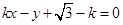 ,
,
设 的方程为
的方程为 ,即
,即 ,
,
∴点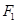 到直线
到直线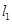 的距离为
的距离为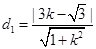 ,
,
点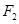 到直线
到直线 的距离为
的距离为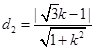 ,
10分
,
10分
∴直线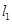 被圆
被圆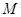 截得的弦长
截得的弦长 , 11分
, 11分
直线 被圆
被圆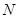 截得的弦长
截得的弦长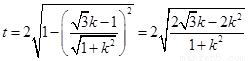 ,
12分
,
12分
∴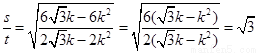 ,
故
,
故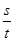 为定值
为定值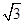 .
14分
.
14分
考点:1.圆锥曲线的定义;2.直线与圆的方程;3.直线与圆的位置关系.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 与双曲线
与双曲线 有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( ) +1 B.
+1 B. +l
+l D.
D.
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 ⊥
⊥ 轴,则双曲线的离心率为
.
轴,则双曲线的离心率为
. 与双曲线
与双曲线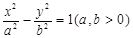 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 轴,若
轴,若 为双曲线的一条斜率大于0的渐近线,则
为双曲线的一条斜率大于0的渐近线,则 (B)
(B) (C)
(C) (D)
(D)
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 .点
.点 是两曲线的一个交点,
是两曲线的一个交点, 轴.若直线
轴.若直线 是双曲线的一条渐近线,则直线
是双曲线的一条渐近线,则直线 B.
B. C.
C. D.
D.
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,
是两曲线的一个交点, 轴,若直线
轴,若直线 是双曲线的一条渐近线,则直线
是双曲线的一条渐近线,则直线 B.
B. C.
C. D.
D.