题目内容
若函数y=x3-2mx2+m2x,当x=
时,函数取得极大值,则m的值为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
| C、1 | ||
| D、都不对 |
分析:先对函数进行求导,然后令导函数等于0求出m的值,再将m的值代入验证是否是极大值点即可.
解答:解:∵y=x3-2mx2+m2x∴y'=3x2-4mx+m2
∵当x=
时,函数取得极大值
∴3×(
)2-4m×
+m2=0∴m=1或
当m=
时,y'=3x2-
x+
=
(3x-1)(9x-1)
当
<x<
时,y'<0,原函数单调递减
当x<
或x>
时,y'>0,原函数单调递增.
故函数在x=
时,函数取得极小值,舍去
同理验证m=1时满足条件.
故选C.
∵当x=
| 1 |
| 3 |
∴3×(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
当m=
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
当
| 1 |
| 9 |
| 1 |
| 3 |
当x<
| 1 |
| 9 |
| 1 |
| 3 |
故函数在x=
| 1 |
| 3 |
同理验证m=1时满足条件.
故选C.
点评:本题主要考查函数的极值与其导函数的关系,即函数取到极值时导函数一定等于0,反之不一定正确.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
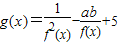 的定义域和值域均是[1,b],求实数a、b的值.
的定义域和值域均是[1,b],求实数a、b的值.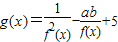 的定义域和值域均是[1,b],求实数a、b的值.
的定义域和值域均是[1,b],求实数a、b的值.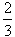 时有极值,求f(x)的单调区间;
时有极值,求f(x)的单调区间;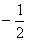 ,求实数m的值。
,求实数m的值。