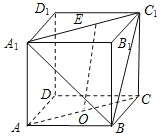
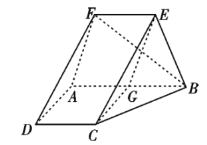
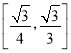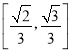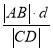题目内容
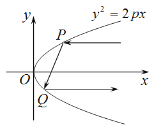
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,过左焦点的直线
,过左焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点(异于
两点(异于![]() 、
、![]() 两点),当直线
两点),当直线![]() 垂直于
垂直于![]() 轴时,四边形
轴时,四边形![]() 的面积为6.
的面积为6.
(1)求椭圆的方程;
(2)设直线![]() 、
、![]() 的交点为
的交点为![]() ;试问
;试问![]() 的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
的横坐标是否为定值?若是,求出定值;若不是,请说明理由.
【答案】(1)![]()
(2)是为定值,![]() 的横坐标为定值
的横坐标为定值![]()
【解析】
(1)根据“直线![]() 垂直于
垂直于![]() 轴时,四边形
轴时,四边形![]() 的面积为6”列方程,由此求得
的面积为6”列方程,由此求得![]() ,结合椭圆离心率以及
,结合椭圆离心率以及![]() ,求得
,求得![]() ,由此求得椭圆方程.
,由此求得椭圆方程.
(2)设出直线![]() 的方程
的方程![]() ,联立直线
,联立直线![]() 的方程和椭圆方程,化简后写出根与系数关系.求得直线
的方程和椭圆方程,化简后写出根与系数关系.求得直线![]() 的方程,并求得两直线交点
的方程,并求得两直线交点![]() 的横坐标,结合根与系数关系进行化简,求得
的横坐标,结合根与系数关系进行化简,求得![]() 的横坐标为定值
的横坐标为定值![]() .
.
(1)依题意可知![]() ,解得
,解得![]() ,即
,即![]() ;而
;而![]() ,即
,即![]() ,结合
,结合![]() 解得
解得![]() ,
,![]() ,因此椭圆方程为
,因此椭圆方程为![]()
(2)由题意得,左焦点![]() ,设直线
,设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() .
.
由![]() 消去
消去![]() 并整理得
并整理得![]() ,∴
,∴![]() ,
,![]() .
.
直线![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为:
的方程为:![]() .
.
联系方程,解得![]() ,又因为
,又因为![]() .
.
所以![]() .所以
.所以![]() 的横坐标为定值
的横坐标为定值![]() .
.

【题目】随着科技的发展,近年看电子书的国人越来越多;所以近期有许多人呼呼“回归纸质书”,目前出版物阅读中纸质书占比出现上升现随机选出200人进行采访,经统计这200人中看纸质书的人数占总人数![]() .将这200人按年龄分成五组:第l组
.将这200人按年龄分成五组:第l组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中统计看纸质书的人得到的频率分布直方图如图所示.
,其中统计看纸质书的人得到的频率分布直方图如图所示.
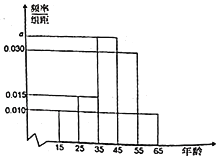
(1)求![]() 的值及看纸质书的人的平均年龄;
的值及看纸质书的人的平均年龄;
(2)按年龄划分,把年龄在![]() 的称青壮年组,年龄在
的称青壮年组,年龄在![]() 的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面
的称为中老年组,若选出的200人中看电子书的中老年人有10人,请完成下面![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为看书方式与年龄层有关?
看电子书 | 看纸质书 | 合计 | |
青壮年 | |||
中老年 | |||
合计 |
附:![]() (其中
(其中![]() ).
).
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |