题目内容
设公比为q(q>0)的等比数列{an}的前n项和为Sn.若S2=3a2+2,S4=3a4+2,则q= _________ .

解析试题分析:由已知可得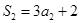 ,
,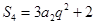 ,两式相减得
,两式相减得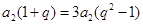 即
即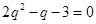 ,解得
,解得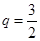 或
或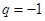 (舍),答案为
(舍),答案为 .
.
考点:等比数列的性质与应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知等比数列{ n}的各项均为正数,公比q≠1,设P=
n}的各项均为正数,公比q≠1,设P= ,Q=
,Q=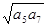 则P与Q的大小关系是( )
则P与Q的大小关系是( )
| A.P>Q | B.P<Q | C.P=Q | D.无法确定 |
数列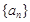 的前n项和为Sn,若
的前n项和为Sn,若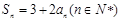 ,则这个数列一定是( )
,则这个数列一定是( )
| A.等比数列 | B.等差数列 |
| C.从第二项起是等比数列 | D.从第二项起是等差数列 |
把公差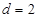 的等差数列
的等差数列 的各项依次插入等比数列
的各项依次插入等比数列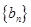 中,将
中,将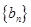 按原顺序分成1项,2项,4项,…,
按原顺序分成1项,2项,4项,…,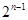 项的各组,得到数列
项的各组,得到数列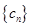 :b1,a1,b2,b3,a2,b4,b5,b6,b7,a3,…,若
:b1,a1,b2,b3,a2,b4,b5,b6,b7,a3,…,若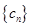 的前n项的和为
的前n项的和为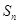 ,且
,且 ,则
,则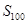 等于( )
等于( )
A. | B. |
C.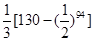 | D.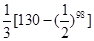 |
在等比数列 中,若公比
中,若公比 ,且
,且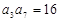 ,
,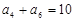 ,则
,则
A.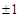 | B.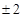 | C.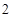 | D.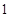 |
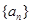 的公比为正数,且
的公比为正数,且 =
= ,
,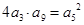 ,则
,则 = .
= . ,则
,则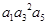 = 。
= 。