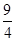题目内容
设正实数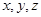 满足
满足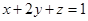 ,则
,则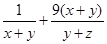 的最小值为 .
的最小值为 .
【答案】
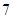
【解析】
试题分析:因为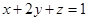 ,所以
,所以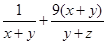 =
=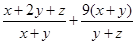 =
= 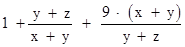
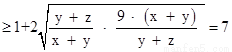 ,当且仅当
,当且仅当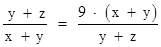 且
且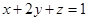
时,取最小值7.
考点:本题主要考查均值定理的应用。
点评:中档题,运用均值定理求最值,要注意“一正、二定、三相等”缺一不可,本解法的优点是,通过改造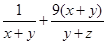 的结构形式,创造了应用均值定理的条件,使问题得解。
的结构形式,创造了应用均值定理的条件,使问题得解。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
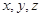 满足
满足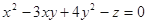 ,则当
,则当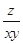 取得最小值时,
取得最小值时,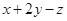 的最大值为 .
的最大值为 .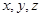 满足
满足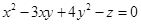 ,则当
,则当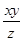 取得最大值时,
取得最大值时,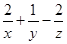 的最大值是(
)
的最大值是(
)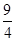 D.
3
D.
3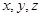 满足
满足 ,则当
,则当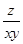 取得最大值时,
取得最大值时, 的最大值为(
)
的最大值为(
) B.
B.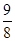 C.
C.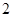 D.
D.