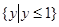题目内容
对于给定的以下四个命题,其中正确命题的个数为( )①函数
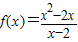 是奇函数;
是奇函数;②函数f(x)在(a,b)和(c,d)都是增函数,若x1∈(a,b),x2∈(c,d),且x1<x2则一定有f(x1)<f(x2);
③函数f(x)在R上为奇函数,且当x>0时有
 ,则当x<0,f(x)=
,则当x<0,f(x)= ;
;④函数
 的值域为{y|y≤1}.
的值域为{y|y≤1}.A.1
B.2
C.3
D.4
【答案】分析:①由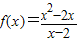 =x(x≠2)的定义域关于原点不对称,可得函数是非奇非偶函数
=x(x≠2)的定义域关于原点不对称,可得函数是非奇非偶函数
②例如y=sinx在(0, ),(2π,
),(2π, )上单调递增,取
)上单调递增,取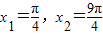 ,但是f(x1)=f(x2),
,但是f(x1)=f(x2),
③函数f(x)在R上为奇函数,且当x>0时有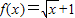 ,则当x<0,-x>0,则可得f(x)=-f(-x)可求
,则当x<0,-x>0,则可得f(x)=-f(-x)可求
④函数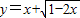 ,令t=
,令t=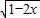 则x=
则x=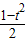 ,且t≥0,从而有
,且t≥0,从而有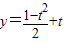 =
=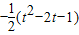 =
=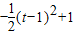 ,利用二次函数的性质可求
,利用二次函数的性质可求
解答:解:①∵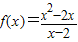 =x(x≠2)的定义域关于原点不对称,故函数是非奇非偶函数,①错误
=x(x≠2)的定义域关于原点不对称,故函数是非奇非偶函数,①错误
②函数f(x)在(a,b)和(c,d)都是增函数,若x1∈(a,b),x2∈(c,d),且x1<x2则一定有f(x1)<f(x2)错误,例如y=sinx在(0,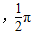 ),(2π,
),(2π,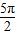 )上单调递增,取
)上单调递增,取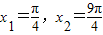 ,但是f(x1)=f(x2),故②错误.
,但是f(x1)=f(x2),故②错误.
③函数f(x)在R上为奇函数,且当x>0时有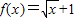 ,则当x<0,-x>0,则可得f(x)=-f(-x)=
,则当x<0,-x>0,则可得f(x)=-f(-x)=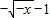 ,故③正确
,故③正确
④函数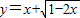 ,令t=
,令t=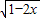 则x=
则x=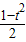 ,且t≥0,
,且t≥0,
∴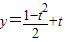 =
=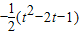 =
=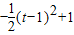
当t=1时,函数有最大值1,即函数的值域为{y|y≤1}故④正确
故选B
点评:本题主要考查了函数奇偶性的判定,解题中不要漏掉函数定义域的考虑,函数单调性的应用,及由奇函数的性质求解函数解析式,利用换元法求解函数的值域,综合考查了函数的性质的应用.
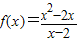 =x(x≠2)的定义域关于原点不对称,可得函数是非奇非偶函数
=x(x≠2)的定义域关于原点不对称,可得函数是非奇非偶函数②例如y=sinx在(0,
 ),(2π,
),(2π,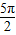 )上单调递增,取
)上单调递增,取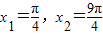 ,但是f(x1)=f(x2),
,但是f(x1)=f(x2),③函数f(x)在R上为奇函数,且当x>0时有
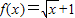 ,则当x<0,-x>0,则可得f(x)=-f(-x)可求
,则当x<0,-x>0,则可得f(x)=-f(-x)可求④函数
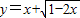 ,令t=
,令t=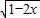 则x=
则x=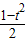 ,且t≥0,从而有
,且t≥0,从而有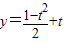 =
=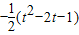 =
=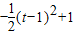 ,利用二次函数的性质可求
,利用二次函数的性质可求解答:解:①∵
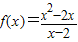 =x(x≠2)的定义域关于原点不对称,故函数是非奇非偶函数,①错误
=x(x≠2)的定义域关于原点不对称,故函数是非奇非偶函数,①错误②函数f(x)在(a,b)和(c,d)都是增函数,若x1∈(a,b),x2∈(c,d),且x1<x2则一定有f(x1)<f(x2)错误,例如y=sinx在(0,
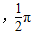 ),(2π,
),(2π,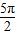 )上单调递增,取
)上单调递增,取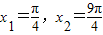 ,但是f(x1)=f(x2),故②错误.
,但是f(x1)=f(x2),故②错误.③函数f(x)在R上为奇函数,且当x>0时有
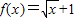 ,则当x<0,-x>0,则可得f(x)=-f(-x)=
,则当x<0,-x>0,则可得f(x)=-f(-x)=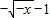 ,故③正确
,故③正确④函数
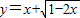 ,令t=
,令t=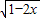 则x=
则x=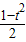 ,且t≥0,
,且t≥0,∴
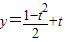 =
=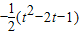 =
=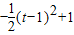
当t=1时,函数有最大值1,即函数的值域为{y|y≤1}故④正确
故选B
点评:本题主要考查了函数奇偶性的判定,解题中不要漏掉函数定义域的考虑,函数单调性的应用,及由奇函数的性质求解函数解析式,利用换元法求解函数的值域,综合考查了函数的性质的应用.

练习册系列答案
相关题目
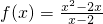 是奇函数;
是奇函数;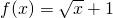 ,则当x<0,f(x)=
,则当x<0,f(x)=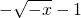 ;
;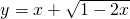 的值域为{y|y≤1}.
的值域为{y|y≤1}.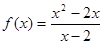 是奇函数;
是奇函数;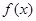 在
在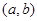 和
和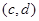 都是增函数,若
都是增函数,若 ,且
,且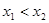 则一定有
则一定有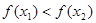 ;
;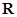 上为奇函数,且当
上为奇函数,且当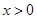 时有
时有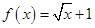 ,则当
,则当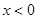 ,
,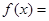
 ;
;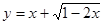 的值域为
的值域为