题目内容
求函数y=2tan( -2x)的定义域、值域、对称中心、并指出它的周期、奇偶性和单调性.
-2x)的定义域、值域、对称中心、并指出它的周期、奇偶性和单调性.
 -2x)的定义域、值域、对称中心、并指出它的周期、奇偶性和单调性.
-2x)的定义域、值域、对称中心、并指出它的周期、奇偶性和单调性.解;
因为 -2x
-2x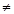 k
k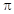 +
+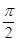 ,所以2x
,所以2x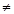 k
k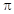 +
+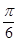 ,所以x
,所以x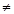
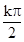 +
+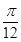 ,
,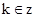
而由于函数y=tanx的值域为R,因此y=2tan( -2x)的值域也是R,
-2x)的值域也是R,
因为y=tanx的对称中心即为(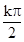 ,0),所以y=2tan(
,0),所以y=2tan( -2x)对称中心为
-2x)对称中心为
(-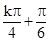 ,0),
,0),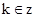
而利用周期公式T=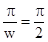 ,因为f(-x)
,因为f(-x) 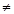 f(x), f(-x)
f(x), f(-x) 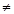 -f(x)因此是非奇函数也非偶函数。
-f(x)因此是非奇函数也非偶函数。
而当 -2x
-2x 时,函数单调递减,则减区间为
时,函数单调递减,则减区间为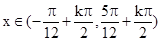
因为
 -2x
-2x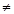 k
k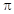 +
+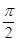 ,所以2x
,所以2x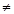 k
k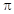 +
+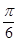 ,所以x
,所以x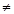
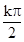 +
+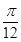 ,
,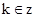
而由于函数y=tanx的值域为R,因此y=2tan(
 -2x)的值域也是R,
-2x)的值域也是R,因为y=tanx的对称中心即为(
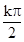 ,0),所以y=2tan(
,0),所以y=2tan( -2x)对称中心为
-2x)对称中心为(-
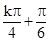 ,0),
,0),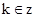
而利用周期公式T=
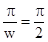 ,因为f(-x)
,因为f(-x) 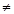 f(x), f(-x)
f(x), f(-x) 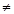 -f(x)因此是非奇函数也非偶函数。
-f(x)因此是非奇函数也非偶函数。而当
 -2x
-2x 时,函数单调递减,则减区间为
时,函数单调递减,则减区间为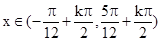
略

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
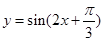 的图象可以将函数
的图象可以将函数 的图象
的图象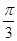 个单位
个单位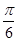 个单位
个单位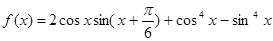
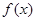 的最小正周期;
的最小正周期; ,求
,求 =1+
=1+ +cos
+cos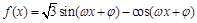 (
(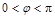 ,
,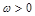 )为偶函数,若对于任意
)为偶函数,若对于任意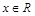 都有
都有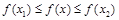 成立,且
成立,且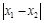 的最小值是为
的最小值是为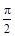 .将函数
.将函数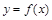 的图象向右平移
的图象向右平移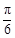 个单位后,得到函数
个单位后,得到函数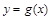 ,求
,求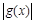 的单调递减区间,确定其对称轴。
的单调递减区间,确定其对称轴。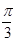 )的图象向左平移
)的图象向左平移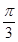 个单位,再将图象上各点的横坐标压缩到原来的
个单位,再将图象上各点的横坐标压缩到原来的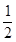 ,那么所得到的图象的解析表达式为 ( )
,那么所得到的图象的解析表达式为 ( ) 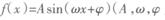 为常数,
为常数,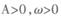 )的部分图象如图所示,则f(0)=
)的部分图象如图所示,则f(0)=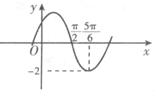
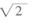
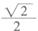
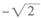
 ,把
,把 的图象按向量
的图象按向量 平移后,图象恰好为函数
平移后,图象恰好为函数 的图象,则
的图象,则 的值可以为 ( )
的值可以为 ( ) 



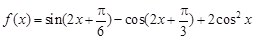 .
. 的值;
的值;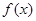 的最大值及相应
的最大值及相应 的值.
的值.