题目内容
 (文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.
(文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.(1)求异面直线A1B与AC所成角的大小;
(2)若直线AM与平面ABC所成角为
| π | 4 |
分析:(1)利用异面直线所成角的定义再结合正四棱柱ABCD-A1B1C1D1中的性质可得直线A1B与A1C1所成的角即为所求然后在三角形A1C1B利用余弦定理即可得解.
(2)由于多面体ABM-A1B1C1的不规则性故可利用VABM-A1B1C1=VABC-A1B1C1- VM-ABC因此需利用直线AM与平面ABC所成角为
来确定点M的位置后问题就解决了.
(2)由于多面体ABM-A1B1C1的不规则性故可利用VABM-A1B1C1=VABC-A1B1C1- VM-ABC因此需利用直线AM与平面ABC所成角为
| π |
| 4 |
解答: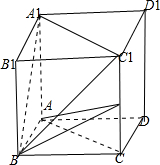 解:(1)连接BC1则由于在正四棱柱ABCD-A1B1C1D1中AC∥A1C1故异面直线A1B与AC所成角即为直线A1B与A1C1所成的角
解:(1)连接BC1则由于在正四棱柱ABCD-A1B1C1D1中AC∥A1C1故异面直线A1B与AC所成角即为直线A1B与A1C1所成的角
∵正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4
∴BC1=2
,A1B=2
,A1C1=2
∴cos∠BA1C1=
=
∴异面直线A1B与AC所成角即为arccos
(2)∵正四棱柱ABCD-A1B1C1D1中MC⊥面ABCD
∴∠MBC=
∵BC=2
∴MC=2
∵VABM-A1B1C1=VABC-A1B1C1- VM-ABC
∴VABM-A1B1C1=
×2×2×4-
×
×2×2×2=
即多面体ABM-A1B1C1的体积为
 解:(1)连接BC1则由于在正四棱柱ABCD-A1B1C1D1中AC∥A1C1故异面直线A1B与AC所成角即为直线A1B与A1C1所成的角
解:(1)连接BC1则由于在正四棱柱ABCD-A1B1C1D1中AC∥A1C1故异面直线A1B与AC所成角即为直线A1B与A1C1所成的角∵正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4
∴BC1=2
| 5 |
| 5 |
| 2 |
∴cos∠BA1C1=
| BA12+A1C12-BC12 |
| 2BA1A1C1 |
| ||
| 10 |
∴异面直线A1B与AC所成角即为arccos
| ||
| 10 |
(2)∵正四棱柱ABCD-A1B1C1D1中MC⊥面ABCD
∴∠MBC=
| π |
| 4 |
∵BC=2
∴MC=2
∵VABM-A1B1C1=VABC-A1B1C1- VM-ABC
∴VABM-A1B1C1=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 20 |
| 3 |
即多面体ABM-A1B1C1的体积为
| 20 |
| 3 |
点评:本题主要考查了异面直线所成的角和几何体体积的求解.解题的关键是第一问要利用图形的性质将异面直线所成的角转化为相交直线所成的角而第二问对于不规则图形体积的求解常采用规则图形的体积差来求解(比如本题中的多面体ABM-A1B1C1的体积转化为正三棱柱的体积减去三棱锥的体积)!

练习册系列答案
相关题目
 是底面边长为1的正四棱柱,高
是底面边长为1的正四棱柱,高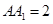 .求:
.求: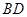 与
与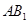 所成的角的大小(结果用反三角函数表示);
所成的角的大小(结果用反三角函数表示);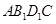 的体积.
的体积.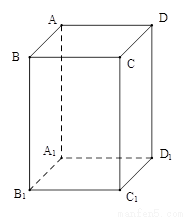
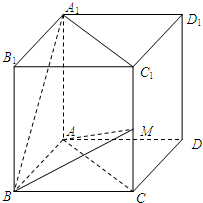 (文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上.
(文科)已知正四棱柱ABCD-A1B1C1D1中,底面边长为2,AA1=4,点M在线段CC1上. ,求多面体ABM-A1B1C1的体积.
,求多面体ABM-A1B1C1的体积.