题目内容
已知函数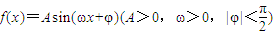 的部分图象如图所示.
的部分图象如图所示.(1)求函数f(x)的解析式;
(2)令
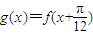 ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.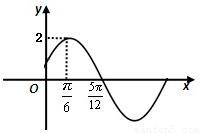
【答案】分析:(1)通过图象容易得到A,求出T,然后利用周期公式求出ω,将点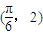 代入f(x)的解析式,求出φ,即可得到函数f(x)的解析式;
代入f(x)的解析式,求出φ,即可得到函数f(x)的解析式;
(2)写出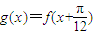 的表达式,选取特殊值
的表达式,选取特殊值 与
与 的函数值的关系,即可判断函数g(x)的奇偶性.
的函数值的关系,即可判断函数g(x)的奇偶性.
解答:解:(Ⅰ)由图象知A=2;f(x)的最小正周期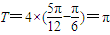 ,
,
故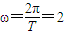 (3分)
(3分)
将点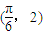 代入f(x)的解析式得
代入f(x)的解析式得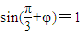 ,
,
又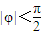 ,∴
,∴
故函数f(x)的解析式为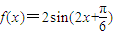 (6分)
(6分)
(Ⅱ)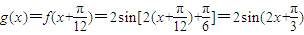 (8分)
(8分)
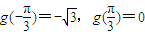
∴ (10分)
(10分)
∴g(-x)≠g(x),g(-x)≠-g(x),g(x)为非奇非偶函数.(12分)
点评:本题是基础题,考查由y=Asin(ωx+φ)的部分图象确定其解析式,此是近几年高考中对三角函数的图象与性质考查的一种较热的题型,注意把握其解题规律.奇偶性的判定方法,也是考点.
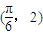 代入f(x)的解析式,求出φ,即可得到函数f(x)的解析式;
代入f(x)的解析式,求出φ,即可得到函数f(x)的解析式;(2)写出
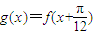 的表达式,选取特殊值
的表达式,选取特殊值 与
与 的函数值的关系,即可判断函数g(x)的奇偶性.
的函数值的关系,即可判断函数g(x)的奇偶性.解答:解:(Ⅰ)由图象知A=2;f(x)的最小正周期
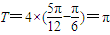 ,
,故
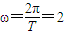 (3分)
(3分)将点
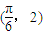 代入f(x)的解析式得
代入f(x)的解析式得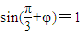 ,
,又
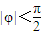 ,∴
,∴
故函数f(x)的解析式为
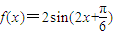 (6分)
(6分)(Ⅱ)
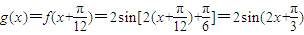 (8分)
(8分)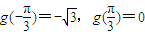
∴
 (10分)
(10分)∴g(-x)≠g(x),g(-x)≠-g(x),g(x)为非奇非偶函数.(12分)
点评:本题是基础题,考查由y=Asin(ωx+φ)的部分图象确定其解析式,此是近几年高考中对三角函数的图象与性质考查的一种较热的题型,注意把握其解题规律.奇偶性的判定方法,也是考点.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 的部分图象如右图所示,设
的部分图象如右图所示,设 是图象的最高点,
是图象的最高点, 是图象与
是图象与 轴的交点,则
轴的交点,则 ( )
( )
 B.
B.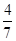 C.
C. D.
D.

 的部分图象如图所示.
的部分图象如图所示. ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
 的部分图象如图所示.
的部分图象如图所示. ,求函数f(x)的值域.
,求函数f(x)的值域.
 的部分图象如图所示,则
的部分图象如图所示,则 的解析式是 ( )
的解析式是 ( ) B.
B.
 D.
D.


 的部分图象如右图所示,则
的部分图象如右图所示,则 的值为________.
的值为________.