题目内容
已知对任意实数x，函数f（x）和g（x）均满足：
，
，证明：对任意实数x，不等式cosf（x）＞sing（x）恒成立．
【答案】分析：根据f（x）和g（x）均满足：
，
，利用不等式的性质得出
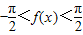
，再根据函数y=sinx的单调性，得sin（
）＞sing（x），由三角函数的诱导公式，即可得得证明．
解答：解：∵f（x）和g（x）均满足：
，①
，②
由②得
，③
①+②得：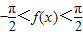
，⇒
，
①+③得：
，
由①得：
，
根据函数y=sinx的单调性，得：
sin（
）＞sing（x），
由三角函数的诱导公式，得
cosf（x）＞sing（x）．
点评：本小题主要考查函数单调性的应用、复合三角函数的单调性、不等式的证明等基础知识，考查运算求解能力，化归与转化思想．属于基础题．
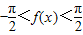
，，利用不等式的性质得出，再根据函数y=sinx的单调性，得sin（）＞sing（x），由三角函数的诱导公式，即可得得证明．解答：解：∵f（x）和g（x）均满足：
，①，②由②得
，③①+②得：
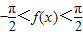，⇒，①+③得：
，由①得：
，根据函数y=sinx的单调性，得：
sin（
）＞sing（x），由三角函数的诱导公式，得
cosf（x）＞sing（x）．
点评：本小题主要考查函数单调性的应用、复合三角函数的单调性、不等式的证明等基础知识，考查运算求解能力，化归与转化思想．属于基础题．
练习册系列答案
星级口算天天练系列答案
相关题目
对任意实数x，函数值恒大于0，实数k的取值范围是________．
对任意实数x，函数值恒大于0，求实数m的取值范围．
对任意实数x，函数值恒大于0，求实数k的取值范围．