题目内容
设l是直线,α,β是两个不同的平面,下列命题中正确的是
①若l∥α,l∥β,则α∥β; ②若l∥α,l⊥β,则α⊥β; ③若α⊥β,l⊥α,则l⊥β; ④若α⊥β,l∥α,则l⊥β.
②
②
①若l∥α,l∥β,则α∥β; ②若l∥α,l⊥β,则α⊥β; ③若α⊥β,l⊥α,则l⊥β; ④若α⊥β,l∥α,则l⊥β.
分析:①若l∥α,l∥β,则α∥β,构造反例;
②若l∥α,l⊥β,则α⊥β;由线面平行的性质定理及面面垂直的判定定理可判断;
③若α⊥β,l⊥α,则l⊥β,构造反例;
④若α⊥β,l∥α,则l⊥β,构造反例;
②若l∥α,l⊥β,则α⊥β;由线面平行的性质定理及面面垂直的判定定理可判断;
③若α⊥β,l⊥α,则l⊥β,构造反例;
④若α⊥β,l∥α,则l⊥β,构造反例;
解答:解:①由l∥α,l∥β,不一定推出α∥β.反例如图:
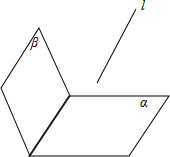 所以①不正确;
所以①不正确;
②如图所示:

过l作平面γ交平面α于直线a,
因为l∥α,所以l∥a,又l⊥β,所以a⊥β,
a?α,故α⊥β,所以②正确;
③由α⊥β,l⊥α,不能推出l⊥β;反例如图:故③不正确;

④若α⊥β,l∥α,未必有l⊥β.反例如图:
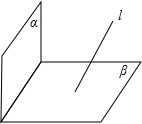 故④不正确;
故④不正确;
 所以①不正确;
所以①不正确;②如图所示:

过l作平面γ交平面α于直线a,
因为l∥α,所以l∥a,又l⊥β,所以a⊥β,
a?α,故α⊥β,所以②正确;
③由α⊥β,l⊥α,不能推出l⊥β;反例如图:故③不正确;

④若α⊥β,l∥α,未必有l⊥β.反例如图:
 故④不正确;
故④不正确;点评:本题考查命题真假的判断及空间中直线与平面、平面与平面之间的位置关系,考查了相关的判定定理及性质定理,本题还考查空间想像能力及运用题设条件组织证明的能力.

练习册系列答案
相关题目
