题目内容
一辆卡车高3m,宽1.6m,欲通过横断面为抛物线形的隧道,已知拱口AB的宽恰好为拱高CD的4倍,|AB|=am,,求能使卡车通过的a的最小整数值.
【答案】分析:建立如图的坐标系,已知拱口AB的宽恰好为拱高CD的4倍,|AB|=am,可得A(-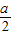 ,-
,-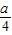 ),B(
),B(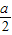 ,-
,-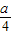 ),由此求出抛物线的方程,再研究车的上部与拱顶恰好接触的情况,求出能使卡车通过的a的最小整数值
),由此求出抛物线的方程,再研究车的上部与拱顶恰好接触的情况,求出能使卡车通过的a的最小整数值
解答: 解:由题意如图,已知拱口AB的宽恰好为拱高CD的4倍,|AB|=am,可得A(-
解:由题意如图,已知拱口AB的宽恰好为拱高CD的4倍,|AB|=am,可得A(-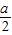 ,-
,-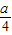 ),B(
),B(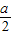 ,-
,-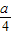 ),设抛物线的标准方程是x2=-2py,代入点A的坐标得
),设抛物线的标准方程是x2=-2py,代入点A的坐标得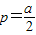
故抛物线的方程是x2=-ay
研究极限情况,一辆卡车高3m,宽1.6m,若上顶E,F恰好在抛物线上,则E(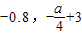 )代入得
)代入得
0.64=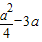 ,解得a=6+
,解得a=6+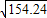
又6<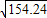 <7
<7
能使卡车通过的a的最小整数值是13
点评:本题考查抛物线的应用,解题的关键是根据抛物线的方程与实际问题相结合,解出抛物线的方程,再由方程求出参数.
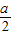 ,-
,-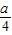 ),B(
),B(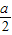 ,-
,-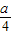 ),由此求出抛物线的方程,再研究车的上部与拱顶恰好接触的情况,求出能使卡车通过的a的最小整数值
),由此求出抛物线的方程,再研究车的上部与拱顶恰好接触的情况,求出能使卡车通过的a的最小整数值解答:
 解:由题意如图,已知拱口AB的宽恰好为拱高CD的4倍,|AB|=am,可得A(-
解:由题意如图,已知拱口AB的宽恰好为拱高CD的4倍,|AB|=am,可得A(-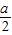 ,-
,-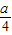 ),B(
),B(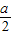 ,-
,-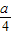 ),设抛物线的标准方程是x2=-2py,代入点A的坐标得
),设抛物线的标准方程是x2=-2py,代入点A的坐标得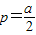
故抛物线的方程是x2=-ay
研究极限情况,一辆卡车高3m,宽1.6m,若上顶E,F恰好在抛物线上,则E(
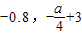 )代入得
)代入得0.64=
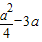 ,解得a=6+
,解得a=6+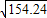
又6<
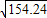 <7
<7能使卡车通过的a的最小整数值是13
点评:本题考查抛物线的应用,解题的关键是根据抛物线的方程与实际问题相结合,解出抛物线的方程,再由方程求出参数.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目