题目内容
(2012•青浦区一模)设集合A={x|
≥0},集合B={x||x-2|>1},且B⊆A,则实数a的取值范围是 ( )
| x-1 |
| x-a |
分析:解|x-2|>1可得集合B,对于A,先将
≥0转化为(x-1)(x-a)≥0且x≠a,分a=1,a>1,a<1三种情况讨论,求出集合A,判断B⊆A是否成立,综合可得a的范围,即可得答案.
| x-1 |
| x-a |
解答:解:|x-2|>1?x<1或x>3,则B={x|x<1或x>3},
对于A,
≥0?(x-1)(x-a)≥0且x≠a,
①a=1时,A={x|x≠1},B⊆A成立,符合题意,
②a<1时,A={x|x<a或x≥1},B⊆A不会成立,不符合题意,
③a>1时,A={x|x>a或x≤1},
要使B⊆A成立,必有a≤3,则a的范围是1<a≤3,
综合①②③可得,a的取值范围为1≤a≤3;
故选C.
对于A,
| x-1 |
| x-a |
①a=1时,A={x|x≠1},B⊆A成立,符合题意,
②a<1时,A={x|x<a或x≥1},B⊆A不会成立,不符合题意,
③a>1时,A={x|x>a或x≤1},
要使B⊆A成立,必有a≤3,则a的范围是1<a≤3,
综合①②③可得,a的取值范围为1≤a≤3;
故选C.
点评:本题考查集合之间关系的判断,涉及分式、绝对值不等式的解法,解分式不等式一般要转化为整式不等式,有参数时,一般要分类讨论.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
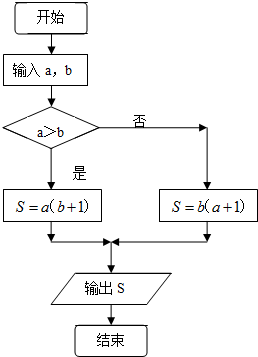 (2012•青浦区一模)定义某种新运算⊙:s=a⊙b的运算原理如图流程图所示,则5⊙4-3⊙4=
(2012•青浦区一模)定义某种新运算⊙:s=a⊙b的运算原理如图流程图所示,则5⊙4-3⊙4= (2012•青浦区一模)如图:三棱锥P-ABC中,PA⊥底面ABC,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为
(2012•青浦区一模)如图:三棱锥P-ABC中,PA⊥底面ABC,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为