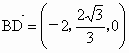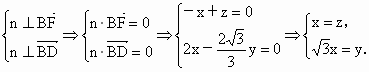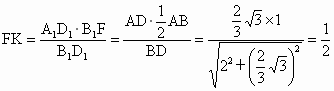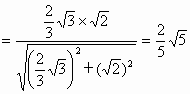题目内容
(2005
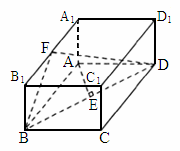
山东,20)如下图,已知长方体 ,AB=2,
,AB=2, ,直线BD与平面
,直线BD与平面 所成的角为30°,AE垂直BD于E,F为
所成的角为30°,AE垂直BD于E,F为 的中点.
的中点.
(1)
求异面直线AE与BF所成的角;(2)
求平面BDF与平面 所成二面角(锐角)的大小;
所成二面角(锐角)的大小;
(3)
求点A到平面BDF的距离.
答案:略
解析:
提示:
解析:
|
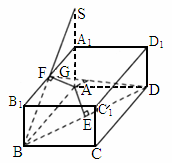
解析:解法一:在长方体  中,以AB所在直线为x轴,AD所在直线为y轴, 中,以AB所在直线为x轴,AD所在直线为y轴,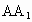 所在直线为z轴建立空间直角坐标系如下图. 所在直线为z轴建立空间直角坐标系如下图.
由已知 AB=2, ,可得A(0,0,0),B(2,0,0),F(1,0,1). ,可得A(0,0,0),B(2,0,0),F(1,0,1).
又 AD⊥平面 ,从而BD与平面 ,从而BD与平面 所成的角即为∠DBA=30°,又AB=2,AE⊥BD,AE=1, 所成的角即为∠DBA=30°,又AB=2,AE⊥BD,AE=1, , ,
从而易得  ,D ,D . .
(1) 因为 , ,
所以  . .
即异面直线 AE、BF所成的角为 . .
(2) 易知平面 的一个法向量m=(0,1,0). 的一个法向量m=(0,1,0).
设 n=(x,y,z)是平面BDF的一个法向量,
取 n=(1, ,1),∴ ,1),∴ , ,
即平面 BDF与平面 所成二面角(锐角)大小为 所成二面角(锐角)大小为 . .
(3) 点A到平面BDF的距离,即 在平面BDF的法向量n上的投影的绝对值. 在平面BDF的法向量n上的投影的绝对值.
所以距离 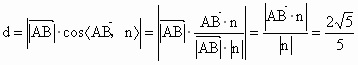 . .
所以点 A到平面BDF的距离为 . .
解法二:如下图.
(1) 连结 ,过F作 ,过F作 的垂线,垂足为K, 的垂线,垂足为K,
∵  与两底面ABCD, 与两底面ABCD, 都垂直, 都垂直,
∴∠ BFK为异面直线BF与AE所成的角.连结BK,由FK⊥面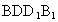 得FK⊥BK,从而△BKF为Rt△. 得FK⊥BK,从而△BKF为Rt△.
在 Rt△ 和Rt△ 和Rt△ 中,由 中,由 得 得
又  ,故 ,故 . .
∴异面直线 BF与AE所成的角为 . .
(2) 如下图,由于DA⊥面 ,由A作BF的垂线AG,垂足为G.连结BG,由三垂线定理知BG⊥DG. ,由A作BF的垂线AG,垂足为G.连结BG,由三垂线定理知BG⊥DG.
∴∠ AGD即为平面BDF与平面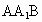 所成二面角的平面角. 所成二面角的平面角.
且∠ DAG=90°.在平面 中,延长BF与 中,延长BF与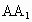 交于点S, 交于点S,
∵ F为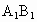 的中点, 的中点, , ,
∴ 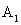 、F分别为SA、SB的中点,即 、F分别为SA、SB的中点,即 . .
∴ Rt△BAS为等腰三角形,垂足G点为斜边SB的中点F,即F、G重合,易得  .在Rt△BAS中, .在Rt△BAS中, , ,
∴  , , . .
平面 BDF与平面 所成二面角(锐角)为 所成二面角(锐角)为 . .
(3) 如下图,由(2)知平面AFD是平面BDF与平面 所成二面角的平面角所在的平面, 所成二面角的平面角所在的平面,
∴面 AFD⊥面BDF.在 Rt△ADF中,由A作AH⊥DF于H,则AH即为点A到平面BDF的距离.由  , ,
得 
所以点 A到平面BDF的距离为 . . |
提示:
|
剖析:本题考查线线角、线面角以及点面距离的求法,可用传统综合法或向量法求解. |

练习册系列答案
相关题目