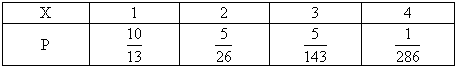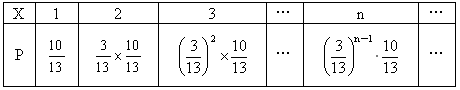Question

从一批有10个合格品与3个次品的产品中，一件一件地抽取产品，设各个产品被抽取到的可能性相同，在下列两种情况下，分别求出直到取出合格品为止时所需抽取次数x的分布列：

(1)每次取出的产品都不放回此批产品中；

(2)每次取出的产品都立即放回此批产品中，然后再取出一件产品．

Answer 1

答案：略
解析：

解析：(1)X的取值为1，2，3，4． 当X=1时，即只取一次就取到合格品，故； 当X=2时，即第一次取到次品，而第二次取到合格品，故 ； 类似地，有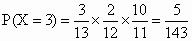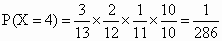；． 可得X的分布列为 (2)X的取值范围为1，2，3，…，n，… 当X=1时，即第一次就取到合格品，故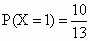； 当X=2时，即第一次就取到次品，而第二次取到合格品，故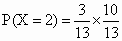； 当X=3时，即第一、二次均取到次品，而第三次取到合格品，故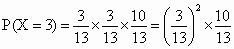； 类似地，当X=n时，即前n－1次均取到次品，而第n次取到合格品，故，n=1，2，3，…． 可得X的分布列为

提示：

最后一次取得合格品，前面均取得次品，然后利用相互独立事件同时发生的概率公式求解．