题目内容
函数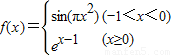 ,若f(1)+f(a)=2,则a的值为: .
,若f(1)+f(a)=2,则a的值为: .
【答案】分析:利用函数f(x)=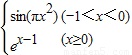 即可求得f(1),再结合f(1)+f(a)=2,可求得f(a)从而可求得a的值.
即可求得f(1),再结合f(1)+f(a)=2,可求得f(a)从而可求得a的值.
解答:解:∵f(x)=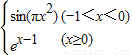 ,
,
∴f(1)=e1-1=e=1,
又f(1)+f(a)=2,
∴f(a)=1;
若-1<a<0,则sin(πa2)=1,
∴πa2=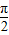 ,
,
∴a=-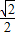 ;
;
若a≥0,则ea-1=1=e,
∴a=1.
综上述,a的值为:1或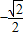 .
.
故答案为:1或-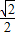 .
.
点评:本题考查函数的值,考查分段函数的理解与应用,考查分类讨论思想与方程思想,属于中档题.
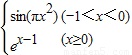 即可求得f(1),再结合f(1)+f(a)=2,可求得f(a)从而可求得a的值.
即可求得f(1),再结合f(1)+f(a)=2,可求得f(a)从而可求得a的值.解答:解:∵f(x)=
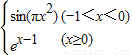 ,
,∴f(1)=e1-1=e=1,
又f(1)+f(a)=2,
∴f(a)=1;
若-1<a<0,则sin(πa2)=1,
∴πa2=
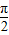 ,
,∴a=-
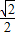 ;
;若a≥0,则ea-1=1=e,
∴a=1.
综上述,a的值为:1或
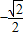 .
.故答案为:1或-
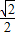 .
.点评:本题考查函数的值,考查分段函数的理解与应用,考查分类讨论思想与方程思想,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目