题目内容
某工厂有一批长为2.5 m的条形钢材,要截成60 cm和42 cm两种规格的零件毛坯,找出最佳的下料方案,并计算材料的利用率.
解:设每根钢材可截成60 cm长的毛坯x根,42 cm长的毛坯y根,据题意得不等式0.6x+0.42y≤2.5. ①
在坐标纸上画出0.6x+0.42y=2.5 ②
的直线,如下图.
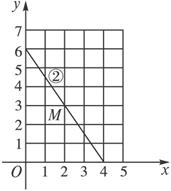
因为要截得的两种毛坯数的和必须是正整数,所以以①的解为坐标的点一定是第一象限内可行域的网格的交点.
如果直线②上有网格的交点,那么按直线上网格交点的坐标(x,y)的值作为下料方案,这时材料全被利用,因此这个方案就是最佳方案,但从上图中可以看出,直线②不能过网格交点,在这种情况下,为了制定最佳下料方案,应该找靠近直线②的网格交点.
当然不能在直线②右上方半平面内找网格交点.右上方半平面内任何网格交点的坐标都使0.6x+0.42y>2.5,这时两种零件毛坯长度的和超过了原钢材长,这是不合理的.这个区域是可行域外的区域,问题的最优解不能在这个区域内.
这样,下料范围只能限制在0.6x+0.42y<2.5表示的可行域区域内.这个区域是直线②下方的左半平面.在直线②的下方左半面上找到最靠近直线的网格交点,得点M(2,3).
x=2,y=3就是所求的最优解,按这样截取毛坯,材料尽管没有被完全利用,但废料最少.
材料的利用率为![]() =98.4%.
=98.4%.
答:把每根钢条截成2根60 cm长和3根42 cm长的零件毛坯是最佳下料方案,材料的利用率为98.4%.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

