题目内容
.设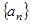 是公差不为零的等差数列,
是公差不为零的等差数列,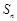 为其前
为其前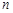 项和,满足:
项和,满足: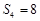 且
且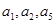 成等比数列.
成等比数列.
(I)求数列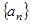 的通项公式;
的通项公式;
(II)设数列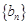 满足:
满足: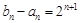 ,
,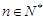 ,
,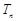 为数列
为数列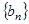 的前
的前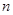 项和,问是否存在正整数
项和,问是否存在正整数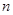 ,使得
,使得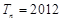 成立?若存在,求出
成立?若存在,求出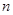 ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】
(I)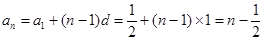 ;
;
(II)不存在正整数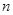 ,使得
,使得 成立。
成立。
【解析】本试题主要是考查了数列通项公式的求解,以及数列求和的综合运用。
(1)因为根据前几项,代入等差数列的通项公式中得到首项和公差,从而得到其通项公式的求解。
(2)由上一问知道数列的通项公式是由一个等差数列和一个等比数列组合而成的,因此采用分组求和的思想得到数列的和的运用。
解:(I)设数列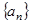 的公差为
的公差为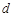 ,且
,且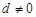
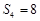 且
且 成等比数列.
成等比数列.
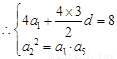 ,即
,即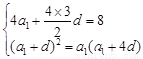
解得 ……3分
……3分
∴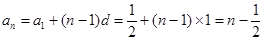 ……6分
……6分
(II)由题知: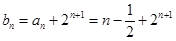 ,
,
∴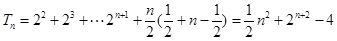 u…………10分
u…………10分
若 ,则
,则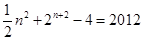 ,即
,即

令 ,知
,知 单调递增,
单调递增,
当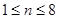 时,
时,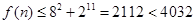
当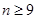 时,
时,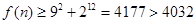 ,
,
故不存在正整数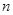 ,使得
,使得 成立。U
…………14分
成立。U
…………14分

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目