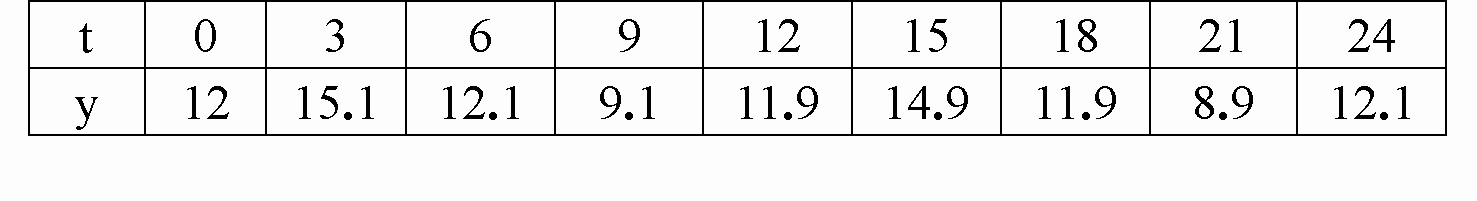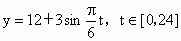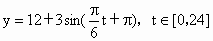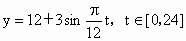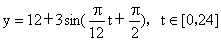题目内容
设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24,下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
T | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
Y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象,下面的函数中,最能近似表示表中数据间对应关系的函数是( )
A.y=12+3sin
t,t∈［0,24］ B.y=12+3sin(
t+π),t∈［0,24］
C.y=12+3sin
t,t∈［0,24］ D.y=12+3sin(
t+
),t∈［0,24］
解析:根据时间t与水深的关系,画出y=f(x)的图象.
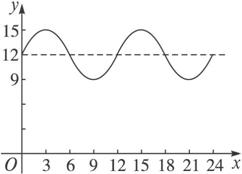
A==3,k==12,T=12,ω==.
∴y=3sin
t+12,t∈［0,24］.
答案:A
设y=f(t)是某港口水的深度关于时间t(时)的函数，其中0≤t≤24,下表是该港口某一天从0至24时记录的时间t与水深y的关系.
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察，函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.
根据上述数据,函数y=f(t)的解析式为( )
A.y=12+3sin
,t∈［0，24］ B.y=12+3sin(
+π),t∈(0,24)
C.y=12+3sin
,t∈［0,24］ D.y=12+3sin(
+
),t∈［0，24］
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )
A.y=12+3sin
t,t∈［0,24］
B.y=12+3sin(
t+π),t∈［0,24］
C.y=12+3sin
t,t∈［0,24］
D.y=12+3sin(
t+
),t∈［0,24］
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数y=f(x)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )
A.y=12+3sin
t,t∈［0,24］ B.y=12+3sin(
t+π),t∈［0,24］
C.y=12+3sin
t,t∈［0,24］ D.y=12+3sin(
t+
),t∈［0,24］