Question

（2012•台州一模）已知l，m表示直线，α，β表示平面，则下列命题中不正确的是（　　）

A．若l∥m，m?α，则l∥α

B．若l∥m，m⊥α，则l⊥α

C．若m⊥α，l⊥α，则l∥m

D．若l⊥α，α∥β，则l⊥β

Answer 1

分析：A．利用线面平行的判断定理去判断．B利用线面垂直的判断定理去判断．C利用线面垂直的性质取判断．D利用线面垂直的判断定理去判断．

解答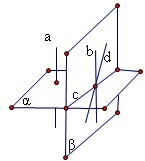：解：A．根据线面平行的判定定理可知当直线和平面平行时，必须要求直线l在平面外，即l?α．所以A错误．
B．由线面垂直的判断定理可知，当l∥m，m⊥α时，有l⊥α，所以B正确．
C．设直线a、b都与平面α垂直，可以用反证法证明a、b必定是平行直线
假设a、b不平行，过直线b与平面α的交点作直线d，使d∥a
∴直线d与直线b是相交直线，设它们确定平面β，且β∩α=c
∵b⊥α，c?α，∴b⊥c．同理可得a⊥c，
又∵d∥a，∴d⊥c
这样经过一点作出两条直线b、d都与直线c垂直，这是不可能的
∴假设不成立，故原命题是真命题
D．若l⊥α，α∥β，则根据一条直线垂直于两个平行平面的一个平面，则必垂直另一个平面，所以必有l⊥β，所以D正确．
故选A．

点评：本题考查线面平行或垂直的判定定理或性质定理．正确理解和应用相应的判断定理或性质定理是解决这类问题的关键．