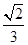题目内容
5.在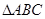 中,
中,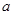 ,
, ,
,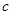 分别是
分别是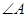 ,
,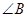 ,
,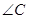 的对边,已知
的对边,已知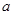 ,
, ,
,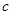 成等比数列,且
成等比数列,且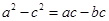 ,则
,则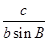 的值为( )
的值为( )
A.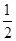 | B.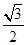 | C.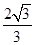 | D.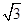 |
C
解析试题分析:因为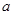 ,
, ,
,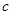 成等比数列,所以
成等比数列,所以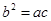 .
.
又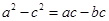 ,∴
,∴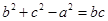 .
.
在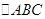 中,由余弦定理得:
中,由余弦定理得: ,那么
,那么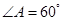 .
.
由正弦定理得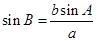 ,又因为
,又因为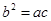 ,
,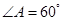 ,
,
所以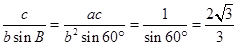 .
.
考点:1、等比数列的性质;2、正弦定理和余弦定理的应用.

练习册系列答案
相关题目
.已知M是△ABC内的一点,且 ,
, ,若△MBC, △MCA和△MAB的面积分别
,若△MBC, △MCA和△MAB的面积分别 ,则
,则 的最小值是 ( )
的最小值是 ( )
| A.9 | B.18 | C.16 | D.20 |
在三角形 中,角
中,角 对应的边分别为
对应的边分别为 ,若
,若 ,
, ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
在△ABC中, ,且
,且 ,则内角C的余弦值为( )
,则内角C的余弦值为( )
| A.1 | B. | C.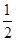 | D. |
在△ 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
在△ 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若 ,则△
,则△ 的面积
的面积 等于( )
等于( )
| A.10 | B.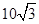 | C.20 | D. |
等腰三角形一腰上的高是 ,这条高与底边的夹角为
,这条高与底边的夹角为 ,则底边长=( )
,则底边长=( )
| A.2 | B. | C.3 | D. |
 且∠ABC=60°,AB=2,BC=4,则球O的表面积为( )
且∠ABC=60°,AB=2,BC=4,则球O的表面积为( ) B.
B. C.
C. D.
D.
 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且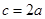 ,则
,则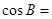 ( )
( )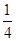 B.
B.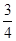 C.
C.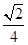 D.
D.