题目内容
已知椭圆G与双曲线12x2-4y2=3有相同的焦点,且过点P(1,
).
(1)求椭圆G的方程;
(2)设F1、F2是椭圆G的左焦点和右焦点,过F2的直线l:x=my+1与椭圆G相交于A、B两点,请问△ABF1的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
| 3 | 2 |
(1)求椭圆G的方程;
(2)设F1、F2是椭圆G的左焦点和右焦点,过F2的直线l:x=my+1与椭圆G相交于A、B两点,请问△ABF1的内切圆M的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
分析:(1)由题意可求椭圆的焦点坐标为F1(-1,0),F2(1,0),2a=|PF1|+|PF2|=4,从而可求a,c,结合以b2=a2-c2可求b,进而可求椭圆G的方程
(2)设△ABF1内切圆M的半径为r,与直线l的切点为C,则三角形S△ABF1=S△ABM+S△AMF1+S△BMF1即S△ABF1=
(|AB|+|AF1|+|BF1|)r=
[(|AF1|+|AF2|)+(|BF1|+|BF2|)]r=2ar=4r,当S△ABF1最大时,r也最大,△ABF1内切圆的面积也最大,而S△ABF1=
|F1F2|•|y1|+
|F1F2|•|y2|=y1-y2,利用方程的根与系数的关系结合函数的性质可求
(2)设△ABF1内切圆M的半径为r,与直线l的切点为C,则三角形S△ABF1=S△ABM+S△AMF1+S△BMF1即S△ABF1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: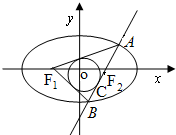 解:(1)双曲线12x2-4y2=3的焦点坐标为(±1,0),所以椭圆的焦点坐标为F1(-1,0),F2(1,0)…(1分)
解:(1)双曲线12x2-4y2=3的焦点坐标为(±1,0),所以椭圆的焦点坐标为F1(-1,0),F2(1,0)…(1分)
设椭圆的长轴长为2a,则2a=|PF1|+|PF2|=4,即a=2,
又c=1,所以b2=a2-c2=3∴椭圆G的方程
+
=1…(5分)
(2)如图,设△ABF1内切圆M的半径为r,与直线l的切点为C,
则S△ABF1=S△ABM+S△AMF1+S△BMF1
即S△ABF1=
(|AB|+|AF1|+|BF1|)r=
[(|AF1|+|AF2|)+(|BF1|+|BF2|)]r=2ar=4r
当S△ABF1最大时,r也最大,△ABF1内切圆的面积也最大,…(7分)
设A(x1,y1)、B(x2,y2)(y1>0,y2<0),则S△ABF1=
|F1F2|•|y1|+
|F1F2|•|y2|=y1-y2,
由
,得(3m2+4)y2+6my-9=0,…(9分)
解得y1=
,y2=
,
∴S△ABF1=
,令t=
,则t≥1,且m2=t2-1,
有S△ABF1=
=
=
,令f(t)=3t+
,则f′(t)=3-
,…(11分)
当t≥1时,f'(t)>0,f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4,S△ABF1≤
=3,
即当t=1,m=0时,4r有最大值3,得rmax=
,这时所求内切圆的面积为
π,…(12分)
∴存在直线l:x=1,△ABF1的内切圆M的面积最大值为
π.…(13分)
 解:(1)双曲线12x2-4y2=3的焦点坐标为(±1,0),所以椭圆的焦点坐标为F1(-1,0),F2(1,0)…(1分)
解:(1)双曲线12x2-4y2=3的焦点坐标为(±1,0),所以椭圆的焦点坐标为F1(-1,0),F2(1,0)…(1分)设椭圆的长轴长为2a,则2a=|PF1|+|PF2|=4,即a=2,
又c=1,所以b2=a2-c2=3∴椭圆G的方程
| x2 |
| 4 |
| y2 |
| 3 |
(2)如图,设△ABF1内切圆M的半径为r,与直线l的切点为C,
则S△ABF1=S△ABM+S△AMF1+S△BMF1
即S△ABF1=
| 1 |
| 2 |
| 1 |
| 2 |
当S△ABF1最大时,r也最大,△ABF1内切圆的面积也最大,…(7分)
设A(x1,y1)、B(x2,y2)(y1>0,y2<0),则S△ABF1=
| 1 |
| 2 |
| 1 |
| 2 |
由
|
解得y1=
-3m+6
| ||
| 3m2+4 |
-3m-6
| ||
| 3m2+4 |
∴S△ABF1=
12
| ||
| 3m2+4 |
| m2+1 |
有S△ABF1=
| 12t |
| 3(t2-1)+4 |
| 12t |
| 3t2+1 |
| 12 | ||
3t+
|
| 1 |
| t |
| 1 |
| t2 |
当t≥1时,f'(t)>0,f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4,S△ABF1≤
| 12 |
| 4 |
即当t=1,m=0时,4r有最大值3,得rmax=
| 3 |
| 4 |
| 9 |
| 16 |
∴存在直线l:x=1,△ABF1的内切圆M的面积最大值为
| 9 |
| 16 |
点评:本题主要考查了由椭圆的性质及定义求解椭圆的方程,直线与椭圆位置关系的应用,难点是计算量较大,是解题中要求考试具备一定的逻辑推理与运算的能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
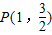 .
.