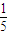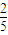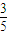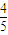题目内容
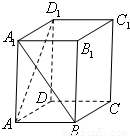
如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )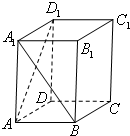

A、
| ||
B、
| ||
C、
| ||
D、
|
分析:先通过平移将两条异面直线平移到同一个起点B,得到的锐角∠A1BC1就是异面直线所成的角,在三角形中A1BC1用余弦定理求解即可.
解答: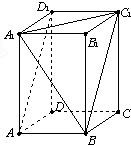 解.如图,连接BC1,A1C1,
解.如图,连接BC1,A1C1,
∠A1BC1是异面直线A1B与AD1所成的角,
设AB=a,AA1=2a,∴A1B=C1B=
a,A1C1=
a,
∠A1BC1的余弦值为
,
故选D.
 解.如图,连接BC1,A1C1,
解.如图,连接BC1,A1C1,∠A1BC1是异面直线A1B与AD1所成的角,
设AB=a,AA1=2a,∴A1B=C1B=
| 5 |
| 2 |
∠A1BC1的余弦值为
| 4 |
| 5 |
故选D.
点评:本题主要考查了异面直线及其所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
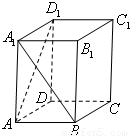 如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )



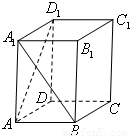 如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )



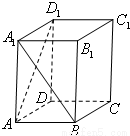 如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )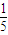
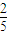
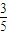
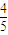
 如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )
如图,正棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为( )