题目内容
已知函数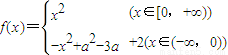 在区间(-∞,+∞)是增函数,则常数a的取值范围是
在区间(-∞,+∞)是增函数,则常数a的取值范围是( )
A.a≤1或a≥2
B.1≤a≤2
C.1<a<2
D.a<1或a>2
【答案】分析:本题函数在区间(-∞,+∞)是增函数,既要在(-∞,0)上增,还要在(0,+∞)上增,还使在(-∞,0)上f(x)的最大值小于等于在(0,+∞)上f(x)的最小值即可.
解答:解:因为函数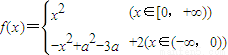 在区间(-∞,+∞)是增函数,
在区间(-∞,+∞)是增函数,
又因f(0)=0,由函数解析式知,在(0,+∞)上与在(-∞,0)上都是增函数,
欲保证函数在R上为增函数,当且仅当a2-3a+2≤0即可,
从而(a-1)(a-2)≤0⇒1≤a≤2.
故选B.
点评:本题考查了分段函数的单调性问题,可以借助图象进行解题,属于易错题.
解答:解:因为函数
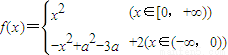 在区间(-∞,+∞)是增函数,
在区间(-∞,+∞)是增函数,又因f(0)=0,由函数解析式知,在(0,+∞)上与在(-∞,0)上都是增函数,
欲保证函数在R上为增函数,当且仅当a2-3a+2≤0即可,
从而(a-1)(a-2)≤0⇒1≤a≤2.
故选B.
点评:本题考查了分段函数的单调性问题,可以借助图象进行解题,属于易错题.

练习册系列答案
相关题目
 在区间
在区间 上为减函数,求实数
上为减函数,求实数 的取值范围为 .
的取值范围为 . 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围是 .
的取值范围是 . 在区间
在区间 上的最大值为
上的最大值为 , 则
, 则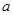 等于( )
等于( ) B.
B.  C.
-
C.
- 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.
