题目内容
设一直线过点A(-1，1)，它被两平行直线l1：x+2y-1=0，l2：x+2y-3=0所截的线段的中点在直线l3：x-y-1=0上，求其方程．
答案：
解析：
解析：
| 解：先设所求直线方程为点斜式，然后利用已知条件用待定系数法确定k．
如图，设所求直线方程l为y-1=k(x+1)． ∵ 点A(-1，1)的坐标满足x+2y-1=0， ∴ 点A(-1，1)是l与l1的交点．
解方程组： ∴ 于是l与l2的交点B的坐标为 AB的中点P(x，y)为
由于P在x-y-1=0上，故 ∵k≠- 有y-1=-
|
(x+1)
练习册系列答案
阅读快车系列答案
相关题目
（a＞b＞0）的离心率e=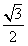
，且过点A（2，0），
过点A且与椭圆的另一交点为B，若|AB|=
，求直线
的倾斜角。 
(
)过点M(1，1)，离心率
，O为坐标原点.
是圆O：
的任意一条切线，且直线
为定值.
(
)过点M(1，1)，离心率
，O为坐标原点.
是圆O：
的任意一条切线，且直线
为定值.