题目内容
已知数列{an}是等差数列，a1=1，a1+a2+…+a20=590
（1）求数列{an}的通项an；
（2）设数列{bn}的通项
（其中a＞0，且a≠1），记Sn是数列{bn}的前n项和．试比较Sn与
的大小，并证明你的结论．
考点：
等差数列的通项公式；数列的求和．
专题：
等差数列与等比数列．
分析：
（1）设数列{an}的公差为d，由题意得
，解之可得首项和公差，可得通项公式；
（2）可得Sn=loga[（1+1）（1+
）…（1+
）]，
=
，问题转化为比较（1+1）（1+
）…（1+
）与
，推测（1+1）（1+）…（1+）＞
，下面由数学归纳法证明，可得最后结论．
解答：
解：（1）设数列{an}的公差为d，由题意得
解得
，所以an=3n﹣2．
（2）．由an=3n﹣2，
，
知Sn=loga（1+1）+loga（1+
）+…+loga（1+
）
=loga[（1+1）（1+
）…（1+）]，
=
=
要比较Sn与
logaan+1的大小，先比较（1+1）（1+
）…（1+
）与
取n=1有（1+1）＞
，取n=2有（1+1）（1+）＞
，…，
由此推测（1+1）（1+）…（1+
）＞
． ①
若①式成立，则由对数函数性质可断定：当a＞1时，Sn＞
logaan+1；当0＜a＜1时，Sn＜logaan+1
下面用数学归纳法证明①式．
（ⅰ）当n=1时已验证①式成立．
（ⅱ）假设当n=k（k≥1）时，①式成立，即（1+1）（1+
）…（1+
）＞
．
那么，当n=k+1时，（1+1）（1+
）…（1+
）（1+
）＞
（1+
）=
（3k+2）．
因为
=
=
，
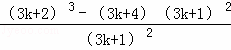所以
（3k+2）＞
．
因而（1+1）（1+
）…（1+
）（1+
）＞
．
这就是说①式当n=k+1时也成立．
由（ⅰ），（ⅱ）知①式对任何正整数n都成立．由此证得：
当a＞1时，Sn＞
logaan+1；当0＜a＜1时，Sn＜logaan+1
由于①等价于k＜g（α），k∈Z
∴k的最大值为2
点评：
本题考查等差数列的通项公式，涉及数学归纳法的应用，属中档题．
每日10分钟口算心算速算天天练系列答案