题目内容
求证:3n＞(n+2)·2n-1（n∈N*，n＞2）.
证明略
证明 利用二项式定理3n=(2+1)n展开证明.
因为n∈N*，且n＞2,所以3n=(2+1)n展开后至少有4项.
（2+1）n=2n+C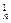
·2n-1+…+C
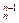·2+1≥2n+n·2n-1+2n+1＞2n+n·2n-1=(n+2)·2n-1,
故3n＞(n+2)·2n-1.
因为n∈N*，且n＞2,所以3n=(2+1)n展开后至少有4项.
（2+1）n=2n+C
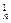·2n-1+…+C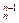·2+1≥2n+n·2n-1+2n+1＞2n+n·2n-1=(n+2)·2n-1,故3n＞(n+2)·2n-1.
练习册系列答案
相关题目
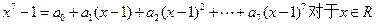恒成立，则
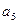值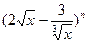
的展开式中含有常数项，则正整数n的最小值是 。
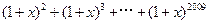的展开式中的
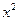系数等于 （ ）
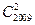
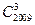
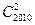
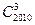
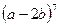的展开式中的第5项的二项式系数是 _______,第5项的系数是_______,第5项是___________.
（
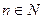）的整数部分和小数部分分别为
和
，则
的值为 （ ）
有关的数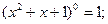
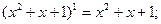
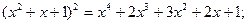
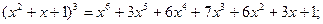
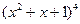展开式中，系数最大项是________。
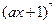的展开式中，
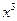的系数是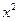
的系数与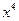
的系数的等差中项，若实数
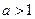，则
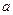的值为 ．