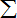题目内容
对于变量x与y,现在随机得到4个样本点A1(2,1),A2(3,2),A3(5,6),A4(4,5).小马同学通过研究后,得到如下结论:
(1)四个样本点的散点图是一个平行四边形的四个顶点;
(2)平行四边形A1A2A3A4的两条对角线A1A3、A2A4所在的直线均可以作为这组样本点的以变量x为解释变量的用最小二乘法求出的回归直线,所不同的是这两条回归直线所对应的回归方程的预报精度不同.你认为上述结论正确吗?试说明理由.(参考数据:
xk=14,
xk2=54,
yk=14,
xkyk=58)
(1)四个样本点的散点图是一个平行四边形的四个顶点;
(2)平行四边形A1A2A3A4的两条对角线A1A3、A2A4所在的直线均可以作为这组样本点的以变量x为解释变量的用最小二乘法求出的回归直线,所不同的是这两条回归直线所对应的回归方程的预报精度不同.你认为上述结论正确吗?试说明理由.(参考数据:
| 4 |
 |
| k=1 |
| 4 |
 |
| k=1 |
| 4 |
 |
| k=1 |
| 4 |
 |
| k=1 |
分析:(1)是一个正确的结论,在四个点组成的四边形中,做出对边的斜率,得到两条直线的斜率相等,得到四边形的两对对边平行,即四边形是一个平行四边形.
(2)这个结论不正确,做出的线性回归直线的方程与两条对角线的方程中对应的直线的斜率差别比较大,首先做出四个点对应的线性回归方程的斜率,再做出两条对角线的斜率,比较得到结论.
(2)这个结论不正确,做出的线性回归直线的方程与两条对角线的方程中对应的直线的斜率差别比较大,首先做出四个点对应的线性回归方程的斜率,再做出两条对角线的斜率,比较得到结论.
解答:解:(1)是一个正确的结论,
∵在四个点组成的四边形中,对边的斜率之间
kA1A2=1=kA3A4
kA2A3=2=kA1A4
∴四边形的两对对边平行,
∴四边形是一个平行四边形,
即第一个结论正确.
(2)这个结论不正确,做出的线性回归直线的方程与两条对角线的方程中对应的直线的斜率差别比较大
首先做出四个点对应的线性回归方程的斜率,
∵
xk2=54,
yk=14,
xkyk=58
xk=14
∴
=1.8
∵kA1A3=
kA2A4=3
∴从三条直线的斜率上可以看出三条直线之间差距较大,不能用平行四边形A1A2A3A4的两条对角线A1A3、A2A4所在的直线作这组样本点的以变量x为解释变量的用最小二乘法求出的回归直线.
∵在四个点组成的四边形中,对边的斜率之间
kA1A2=1=kA3A4
kA2A3=2=kA1A4
∴四边形的两对对边平行,
∴四边形是一个平行四边形,
即第一个结论正确.
(2)这个结论不正确,做出的线性回归直线的方程与两条对角线的方程中对应的直线的斜率差别比较大
首先做出四个点对应的线性回归方程的斜率,
∵
| 4 |
 |
| k=1 |
| 4 |
 |
| k=1 |
| 4 |
 |
| k=1 |
| 4 |
 |
| k=1 |
∴
 |
| b |
∵kA1A3=
| 5 |
| 3 |
kA2A4=3
∴从三条直线的斜率上可以看出三条直线之间差距较大,不能用平行四边形A1A2A3A4的两条对角线A1A3、A2A4所在的直线作这组样本点的以变量x为解释变量的用最小二乘法求出的回归直线.
点评:本题看出独立性检验的应用,看出最小二乘法来求线性回归方程,本题解题的关键是题干比较长需要读懂题意,本题是一个中档题目.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目