题目内容
设函数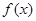 及其导函数
及其导函数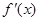 都是定义在R上的函数,则“
都是定义在R上的函数,则“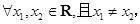
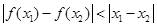 ”是“
”是“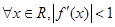 ”的( )
”的( )
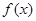 及其导函数
及其导函数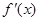 都是定义在R上的函数,则“
都是定义在R上的函数,则“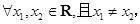
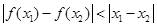 ”是“
”是“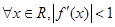 ”的( )
”的( )| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
C
试题分析:由前边的命题成立能推出后边的命题成立,由后边的命题成立也能推出前边的命题成立,由此可得结论.
解答:解:由于
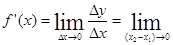
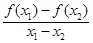 ,故|f′(x)|=
,故|f′(x)|=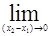
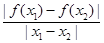 .
.由“
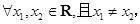
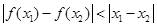 ”,利用函数的导数的定义,可推出|f′(x)|<1,
”,利用函数的导数的定义,可推出|f′(x)|<1,故成分性成立.
再由“
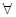 ?x∈R,|f′(x)|<1”,可得“
?x∈R,|f′(x)|<1”,可得“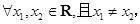
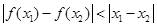 ”成立,
”成立,故必要性成立.
综上可得,“
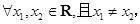
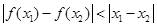 ”是“
”是“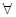 ?x∈R,|f′(x)|<1”的充要条件,
?x∈R,|f′(x)|<1”的充要条件,故选C.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
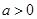 且
且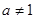 ,命题
,命题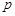 :函数
:函数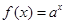 在
在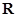 上是增函数 ,命题
上是增函数 ,命题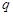 :函数
:函数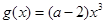 在
在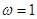 ”是“函数
”是“函数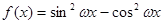 的最小正周期为
的最小正周期为 ”的( ).
”的( ).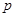 :
: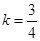 ,条件
,条件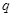 :直线
:直线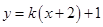 与圆
与圆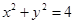 相切,则
相切,则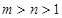 ”是 “
”是 “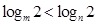 ”的( ).
”的( ).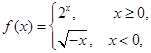 则
则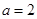 是
是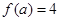 成立的( )
成立的( )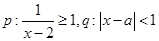 ,若
,若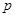 是
是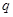 的充分不必要条件,则实数
的充分不必要条件,则实数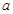 的取值范围为( )
的取值范围为( )