题目内容
(A)直线xcosα+ysinα-sinα-3=0与曲线 的位置关系是 ;
的位置关系是 ;(B)不等式|x+3|+|x-1|≥a2-3a对任意实数x恒成立,则实数a的取值范围为 .
【答案】分析:(A)求出曲线 的圆心坐标与半径,利用圆心到直线的距离与半径比较,即可得到二者的位置关系.
的圆心坐标与半径,利用圆心到直线的距离与半径比较,即可得到二者的位置关系.
(B)利用绝对值的几何意义,求出|x+3|+|x-1|的最小值4,然后求解4≥a2-3a的解集即可.
解答:解:(A)曲线 的圆心坐标(0,1)与半径为:3,圆心到直线xcosα+ysinα-sinα-3=0的距离为:
的圆心坐标(0,1)与半径为:3,圆心到直线xcosα+ysinα-sinα-3=0的距离为: ,
,
所以直线xcosα+ysinα-sinα-3=0与曲线 的位置关系是相切.
的位置关系是相切.
(B)由绝对值的几何意义可知|x+3|+|x-1|≥4,不等式|x+3|+|x-1|≥a2-3a对任意实数x恒成立,所以4≥a2-3a解得:-1≤a≤4.
故答案为:相切;-1≤a≤4
点评:本题是基础题,(A)考查圆的参数方程,直线系与圆的位置关系;(B)考查绝对值的几何意义,不等式的求解;考查计算能力,常考题型.
 的圆心坐标与半径,利用圆心到直线的距离与半径比较,即可得到二者的位置关系.
的圆心坐标与半径,利用圆心到直线的距离与半径比较,即可得到二者的位置关系.(B)利用绝对值的几何意义,求出|x+3|+|x-1|的最小值4,然后求解4≥a2-3a的解集即可.
解答:解:(A)曲线
 的圆心坐标(0,1)与半径为:3,圆心到直线xcosα+ysinα-sinα-3=0的距离为:
的圆心坐标(0,1)与半径为:3,圆心到直线xcosα+ysinα-sinα-3=0的距离为: ,
,所以直线xcosα+ysinα-sinα-3=0与曲线
 的位置关系是相切.
的位置关系是相切.(B)由绝对值的几何意义可知|x+3|+|x-1|≥4,不等式|x+3|+|x-1|≥a2-3a对任意实数x恒成立,所以4≥a2-3a解得:-1≤a≤4.
故答案为:相切;-1≤a≤4
点评:本题是基础题,(A)考查圆的参数方程,直线系与圆的位置关系;(B)考查绝对值的几何意义,不等式的求解;考查计算能力,常考题型.

练习册系列答案
相关题目
若
<α<2π,则直线
+
=1必不经过( )
| 3π |
| 2 |
| x |
| cosα |
| y |
| sinα |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
直线xcosθ+ysinθ-2=0与圆x2+y2=1的位置关系是( )
| A、相离 | B、相交 | C、相切 | D、位置关系与θ有关 |
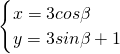 的位置关系是________;
的位置关系是________;