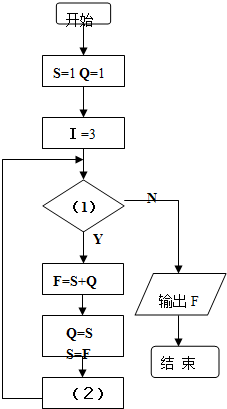
题目内容
1202年，意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系：Fn=Fn-1+Fn-2，其中Fn表示第n个月的兔子的总对数，F1=F2=1，则F8的值为（ ）
分析：根据F1=F2=1，Fn=Fn-1+Fn-2（n≥3，n∈N*），依次另n=3，4，5，6，7，8能够依次求出F3，F4，F5，F6，F7和F8的值．
解答：解：∵F1=F2=1，Fn=Fn-1+Fn-2（n≥3，n∈N*），
∴F3=1+1=2，
F4=2+1=3，
F5=3+2=5，
F6=5+3=8，
F7=5+8=13，
F8=8+13=21
故选B．
∴F3=1+1=2，
F4=2+1=3，
F5=3+2=5，
F6=5+3=8，
F7=5+8=13，
F8=8+13=21
故选B．
点评：本题考查数列递推式的性质和应，解题时要认真审题，仔细解答，注意递推思想的合理运用，属于基础题．
练习册系列答案
相关题目
意大利数学家菲波拉契，在1202年出版的一书里提出了这样的一个问题：
（
），其中
表示第
个月的兔子的总对数，
，则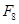
的值为（ ）