题目内容

设A、B、C、D是空间四个不同的点.在下列命题中,不正确的是(    )

A.若AC与BD共面,则AD与BC共面

B.若AC与BD是异面直线,则AD与BC是异面直线

C.若AB=AC,DB=DC,则AD=BC

D.若AB=AC,DB=DC,则AD⊥BC

答案:C

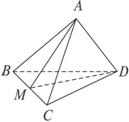
解析:对于选项A,若AC与BD共面,不妨设共面于α,则A、B、C、D∈α.

这样ADα,BCα,则AD与BC共面.

选项B,假设AD与BC为共面直线,由上述A的解析可知AC与BD共面,这与前提“AC与BD为异面直线”矛盾.

故AD与BC是异面直线.

选项D,如图所示,取BC中点M,由AB=AC,DB=DC,得AM⊥BC,DM⊥BC.

又AM∩DM=M,∴BC⊥面AMD.

∴BC⊥AD.

选项C,无法推断.

练习册系列答案
相关题目
7、设A={x|x=2k，k∈Z}，B={x|x=2k+1，k∈Z}，C={x|x=2（k+1），k∈Z}，D={x|x=2k-1，k∈Z}，在A、B、C、D中，哪些集合相等，哪些集合的交集是空集？
（2013•长春一模）对于非空实数集A，记A*={y|?x∈A，y≥x}．设非空实数集合M、P满足：M⊆P，且若x＞1，则x∉P．现给出以下命题：
①对于任意给定符合题设条件的集合M、P，必有P*⊆M*；
②对于任意给定符合题设条件的集合M、P，必有M*∩P≠∅；
③对于任意给定符合题设条件的集合M、P，必有M∩P*=∅；
④对于任意给定符合题设条件的集合M、P，必存在常数a，使得对任意的b∈M*，恒有a+b∈P*，
其中正确的命题是（　　）
设P、Q为两个非空实数集合，定义集合P+Q={a+b|a∈P,b∈Q},若P={0,2,5},Q={1,2,6}，则P+Q中元素的个数是(    )

A.9               B.8            C.7             D.6

设全集为U，若M.N都是U的非空子集，且，则有（     ）

A、          B、

C、      D、

 

设是两个非空实数集合，定义集合.

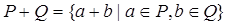若，则中元素的个数是( 　)

A.  9       B. 8      C. 7      D.  6

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网