题目内容
已知p:过点M(2,1)的直线与焦点在x轴上的椭圆
+
=1恒有公共点,q:方程
+
=1表示双曲线,问:p是q的什么条件?并说明理由.
| x2 |
| 6 |
| y2 |
| k |
| x2 |
| k-4 |
| y2 |
| k-6 |
分析:先利用椭圆的标准方程和点在椭圆内,列不等式解得命题p中k的取值范围,即命题p的等价命题,再利用双曲线的标准方程求得命题q的等价命题,最后利用集合法判断两命题的充分必要性
解答:解:∵椭圆
+
=1的焦点在x轴上,∴0<k<6 ①
∵过点M(2,1)的直线与焦点在x轴上的椭圆
+
=1恒有公共点
∴点M(2,1)在椭圆
+
=1内或其上,即
+
≤1 ②
由①②得3≤k<6
∴命题p等价于k∈[-3,6)
∵方程
+
=1表示双曲线
∴(k-4)•(k-6)<0⇒4<k<6,
∴命题q等价于k∈[4,6)
∵[-3,6)?[4,6)
∴p是q的必要不充分条件.
| x2 |
| 6 |
| y2 |
| k |
∵过点M(2,1)的直线与焦点在x轴上的椭圆
| x2 |
| 6 |
| y2 |
| k |
∴点M(2,1)在椭圆
| x2 |
| 6 |
| y2 |
| k |
| 22 |
| 6 |
| 12 |
| k |
由①②得3≤k<6
∴命题p等价于k∈[-3,6)
∵方程
| x2 |
| k-4 |
| y2 |
| k-6 |
∴(k-4)•(k-6)<0⇒4<k<6,
∴命题q等价于k∈[4,6)
∵[-3,6)?[4,6)
∴p是q的必要不充分条件.
点评:本题主要考查了判断命题充分必要性的方法,椭圆和双曲线的标准方程及其应用,点与圆锥曲线的位置关系及其应用,转化化归的思想方法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 恒有公共点,q:方程
恒有公共点,q:方程 表示双曲线,问:p是q的什么条件?并说明理由.
表示双曲线,问:p是q的什么条件?并说明理由. 恒有公共点,q:方程
恒有公共点,q:方程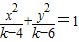 表示双曲线,问:p是q的什么条件?并说明理由.
表示双曲线,问:p是q的什么条件?并说明理由.