Question

（下列两道题任选做一道，若两道都做，则以第一道计分）
（1）正方体ABCD-A₁B₁C₁D₁中，M、N是棱BC、CD的中点，则异面直线AD₁与MN所成的角为    度；
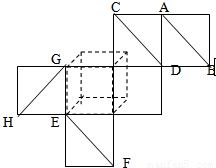
（2）如图是表示一个正方体表面的一种平面展开图，图中的四条线段AB、CD、EF和GH在原正方体中相互异面的有    对．

Answer 1

【答案】分析：（1）连接BD，BC₁，DC₁，将MN平移到BD，将AD₁平移到BC₁，根据异面直线的所成角的定义可知∠DBC₁为异面直线AD₁与MN所成的角，而三角形DBC₁为等边三角形，得到此角．
（2）展开图复原几何体，标出字母即可找出异面直线的对数．
解答：解：（1）连接BD，BC₁，DC₁，MN∥BD，AD₁∥BC₁，
∴∠DBC₁为异面直线AD₁与MN所成的角
而三角形DBC₁为等边三角形
∴∠DBC₁=60°
故答案为：60．
（2）画出展开图复原的几何体，所以C与G重合，F，B重合，
所以：四条线段AB、CD、EF和GH在原正方体中相互异面的有：
AB与GH，AB与CD，GH与EF，
共有3对．
故答案为：3．
点评：（1）本题主要考查异面直线所成的角、异面直线所成的角的求法，考查空间想象能力、运算能力和推理论证能力，考查转化思想，属于基础题．
（2）本题考查几何体与展开图的关系，考查异面直线的对数的判断，考查空间想象能力．