Question

18．作出下列函数一个周期的图象，并指出振幅、周期和初相．
（1）y=3sin（$\frac{1}{2}$x+$\frac{π}{6}$）；
（2）y=$\frac{1}{2}$sin（3x-$\frac{π}{6}$）．

Answer 1

分析 （1）利用五点作图法，得到函数在长度为一个周期的闭区间的简图；根据函数y=Asin（ωx+φ）的图象与有关概念，不难得到函数的振幅，周期，初相．
（2）利用五点作图法，得到函数在长度为一个周期的闭区间的简图；根据函数y=Asin（ωx+φ）的图象与有关概念，不难得到函数的振幅，周期，初相．

解答 解：（1）列出自变量与函数值的对应表格：

$\frac{1}{2}$x+$\frac{π}{6}$	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
x	$-\frac{π}{3}$	$\frac{2π}{3}$	$\frac{5π}{3}$	$\frac{8π}{3}$	$\frac{11π}{3}$
y	0	3	0	-3	0

由此可得在坐标系内描出以上5个点，连成平滑的曲线，得函数在一个周期的闭区间的简图，如下图：

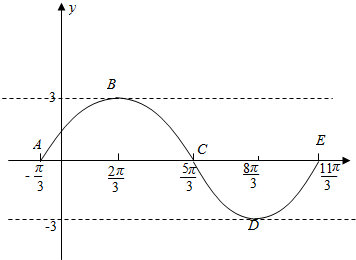
由函数表达式，结合（1）的图象可得
函数的振幅为A=3，周期为T=$\frac{2π}{ω}$=4π，相位为$\frac{1}{2}$x+$\frac{π}{6}$．
（2）列出自变量与函数值的对应表格：

3x-$\frac{π}{6}$	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
x	$\frac{π}{18}$	$\frac{4π}{18}$	$\frac{7π}{18}$	$\frac{10π}{18}$	$\frac{13π}{18}$
y	0	$\frac{1}{2}$	0	-$\frac{1}{2}$	0

由此可得在坐标系内描出以上5个点，连成平滑的曲线，得函数在一个周期的闭区间的简图，如下图
由函数表达式，结合函数的图象可得：

函数的振幅为A=$\frac{1}{2}$，周期为T=$\frac{2π}{ω}$=$\frac{2π}{3}$，相位为3x-$\frac{π}{6}$．

点评 本题给出函数y=Asin（ωx+φ），要求作出函数在一个周期上的简图，着重考查了函数y=Asin（ωx+φ）的图象与性质的知识，属于中档题．