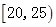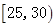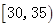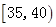题目内容
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如下表所示,| 分组(单位:岁) | 频数 | 频率 |
| [20.25) | 5 | 0.050 |
| [25.30) | ① | 0.200 |
| [30.35) | 35 | ② |
| [35.40) | 30 | 0.300 |
| [40.45) | 10 | 0.100 |
| 合计 | 100 | 1.00 |
(Ⅱ)根据频率分布直方图估计这507名画师中年龄在[30,35)岁的人数(结果取整数);
(Ⅲ)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动,其中选取2名画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为ξ,求ξ的分布列及数学期望.

【答案】分析:(Ⅰ)根据频率分布表,计算①②的数值.
(Ⅱ)根据频率分布直方图估计年龄在[30,35)岁的人数.(Ⅲ)计算出随机变量的分布列,利用数学期望公式求期望.
解答:解:(Ⅰ)20,0.350
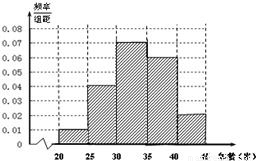
(Ⅱ)507名画师中年龄在[30,35)岁的人数为0.35×507≈177,补全频率分布直方图如图所示:
(Ⅲ)用分层抽样法抽取20人,其中年龄低于30岁”的人数为5人,年龄不低于30岁”的人数为15人,故ξ可能值为0,1,2.
则 ,
,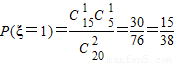 ,
, ,
,
故ξ的分布列为:
所以Eξ= .
.
点评:本题主要考概率和统计的综合应用,利用概率公式计算出随机变量的概率,然后列出概率分布列,然后求出期望.考查学生的运算能力.综合性较强.
(Ⅱ)根据频率分布直方图估计年龄在[30,35)岁的人数.(Ⅲ)计算出随机变量的分布列,利用数学期望公式求期望.
解答:解:(Ⅰ)20,0.350
(Ⅱ)507名画师中年龄在[30,35)岁的人数为0.35×507≈177,补全频率分布直方图如图所示:

(Ⅲ)用分层抽样法抽取20人,其中年龄低于30岁”的人数为5人,年龄不低于30岁”的人数为15人,故ξ可能值为0,1,2.
则
 ,
,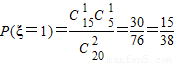 ,
, ,
,故ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | 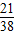 |  | 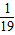 |
 .
.点评:本题主要考概率和统计的综合应用,利用概率公式计算出随机变量的概率,然后列出概率分布列,然后求出期望.考查学生的运算能力.综合性较强.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如表所示.
| 分组 (单位:岁) |
频数 | 频率 |
| [20,25) | 5 | 0.050 |
| [25,30) | ① | 0.200 |
| [30,35) | 35 | ② |
| [35,40) | 30 | 0.300 |
| [40,45] | 10 | 0.100 |
| 合计 | 100 | 1.00 |
(Ⅱ)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会深圳馆志愿者活动,其中选取2名画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为ξ,求ξ的分布列及数学期望.
(本小 题满分12分)
题满分12分)
上海世 博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅
博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅
油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如下表所示.
|
分 组 (单位:岁) |
频数 |
频 率 |
|
|
5 |
0.050 |
|
|
① |
0.200 |
|
|
35 |
② |
|
|
30 |
0.300 |
|
|
10 |
0.100 |
|
合 计 |
100 |
1.00 |
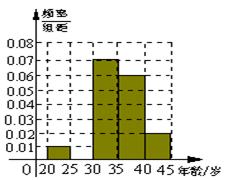
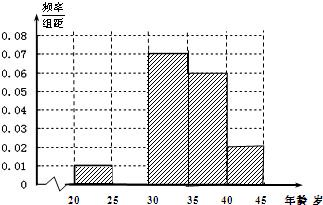
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图,
再根据频率分布直方图估计这507名画师中年龄 在
在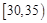 岁的人数(结果取整数);
岁的人数(结果取整数);
(2)在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会 深
深
圳馆志愿者活动,其中选取2名 画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为
画师担任解说员工作,记这2名画师中“年龄低于30岁”的人数为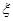 ,求
,求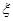 的分布列及数学期望.
的分布列及数学期望.
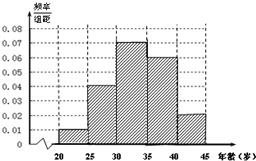 11、上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.根据如图所示的频率分布直方图,估计这507个画师中年龄在[30,35)岁的人数约为
11、上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.根据如图所示的频率分布直方图,估计这507个画师中年龄在[30,35)岁的人数约为
 上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如下表所示,
上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.某部门从参加创作的507名画师中随机抽出100名画师,测得画师年龄情况如下表所示,