题目内容
已知向量a=(3cosα,sinα),α∈(0,π2),e=(1,0),向量a与e的夹角为β,求tan(α-β)的最大值,并求相应的α的值.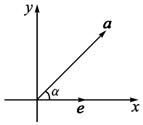
解:由已知:tanβ=![]() =
=![]() tanα.
tanα.
∴tan(α-β)=![]() =
=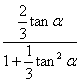 .
.
∵α∈(0,![]() )∴tanα>0.∴tan(α-β)=
)∴tanα>0.∴tan(α-β)=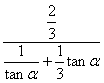 ≤
≤![]() /
/![]() =
=![]() .
.
当且仅当![]() tanα即α=
tanα即α=![]() 时,tan(α-β)有最大值
时,tan(α-β)有最大值![]() .
.

练习册系列答案
相关题目
已知向量
=(3cosα,2),
=(3,4sinα),且
∥
,则锐角α等于( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|