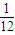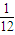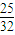Question

6名志愿者随机进入2个不同的全运场馆参加接待工作，则每个场馆至少有两名志愿者的概率为（　　）

• A、

  1

  3

• B、

  1

  12

• C、

  3

  4

• D、

  25

  32

Answer 1

分析：本题是一个等可能事件的概率，试验发生包含的事件是6名志愿者随机进入2个不同的全运场馆，共有2⁶种结果，满足条件的事件是每个场馆至少有两名志愿者，则包括2，4和3，3两种情况，写出事件数，得到概率．

解答：解：由题意知，本题是一个等可能事件的概率，
试验发生包含的事件是6名志愿者随机进入2个不同的全运场馆，共有2⁶=64种结果，
满足条件的事件是每个场馆至少有两名志愿者，则包括2，4和3，3两种情况，
当两个场馆按照2，4分配时，有C₆²A₂²=30，
当两个场馆按照3，3分配时，有C₆³=20，
∴满足条件的事件共有30+20=50种结果，
根据等可能事件的概率公式得到P=

50

64

=

25

32

，
故选D．

点评：本题考查等可能事件的概率，考查平均分组问题，在两个场馆按照3，3分配6名志愿者时，首先有一个平均分组，即

C 3 6 C 3 3

A 2 2

，然后再进行排列．