题目内容
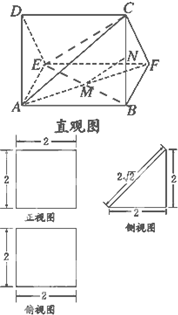 一多面体的直观图及三视图如图所示:(其中M、N分别是EB、BC的中点).
一多面体的直观图及三视图如图所示:(其中M、N分别是EB、BC的中点).(1)求证:MN∥平面CDEF;
(2)求三棱锥A-DEF的体积.
分析:(1)根据线面平行的判定定理只需证明MN∥EC;
(2)由三视图及直观图可以知道:AE=DE=EF=2,由图知VA-DEF=VF-ADE,根据锥体的体积公式即可求出.
(2)由三视图及直观图可以知道:AE=DE=EF=2,由图知VA-DEF=VF-ADE,根据锥体的体积公式即可求出.
解答:解:(1)因为M、N分别为EB、BC的中点,
所以MN∥EC,
又MN?面CDEF,EC?面CDEF,
所以MN∥面CDEF.
(2)由三视图及直观图可以知道:
AE=DE=EF=2,
该几何体为直三棱柱ADE-BCF,且AE⊥DE,
所以VA-DEF=VF-ADE=
×S△ADE×EF
=
×
×AE×DE×EF
=
×
×2×2×2
=
.
所以MN∥EC,
又MN?面CDEF,EC?面CDEF,
所以MN∥面CDEF.
(2)由三视图及直观图可以知道:
AE=DE=EF=2,
该几何体为直三棱柱ADE-BCF,且AE⊥DE,
所以VA-DEF=VF-ADE=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 4 |
| 3 |
点评:本题考查线面平行的判定、锥体体积的求解,考查学生运算能力,考查转化思想的运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 一多面体的直观图及三视图如图所示:(其中M、N分别是EB、BC的中点).
一多面体的直观图及三视图如图所示:(其中M、N分别是EB、BC的中点).