题目内容
在0到1之间随机选择两个数,这两个数对应的点把0到1之间的线段分成了三条线段,这三条线段能构成三角形的概率为( )
分析:先设线段其中两段的长度分别为x、y,分别表示出线段随机地折成3段的x,y的约束条件和3段构成三角形的约束条件,再画出约束条件表示的平面区域,利用面积测度即可求出构成三角形的概率.
解答: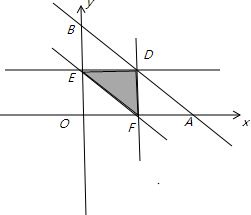 解:设三段长分别为x,y,1-x-y,
解:设三段长分别为x,y,1-x-y,
则总样本空间为
,所表示的平面区域为三角形OAB,其面积为
,
能构成三角形的事件的空间为
,所表示的平面区域为三角形DEF,其面积为
,
则所求概率为
=
.
故选B.
 解:设三段长分别为x,y,1-x-y,
解:设三段长分别为x,y,1-x-y,则总样本空间为
|
| 1 |
| 2 |
能构成三角形的事件的空间为
|
| 1 |
| 8 |
则所求概率为
| S△DEF |
| S△AOB |
| 1 |
| 4 |
故选B.
点评:本题考查几何概型,对于几何概型的问题,一般要通过把试验发生包含的事件同集合结合起来,根据集合对应的图形做出面积,用面积的比值得到结果.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目







