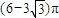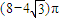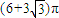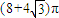题目内容
两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部,且互相外切,若球O1与过点A的正方体的三个面相切,球O2与过点C1的正方体的三个面相切,则球O1和O2的表面积之和的最小值为
- A.
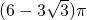
- B.
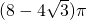
- C.
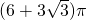
- D.
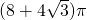
A
分析:设出球O1与球O2的半径,求出面积之和,利用相切关系得到半径与正方体的对角线的关系,通过基本不等式,从而得出面积的最小值.
解答:设球O1与球O2的半径分别为r1,r2,∴r1+r2+ (r1+r2)=
(r1+r2)= .r1+r2=
.r1+r2=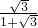 =
=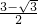 ,
,
r1+r2≥2 ,球O1与球O2的面积之和为:
,球O1与球O2的面积之和为:
S=4π(r12+r22)=4π(r1+r2)2-8πr1r2≥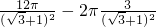
=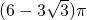 ,当且仅当r1=r2时取等号
,当且仅当r1=r2时取等号
其面积最小值为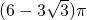 .
.
故选A.
点评:本题是中档题,考查球与正方体相切关系的应用,考查基本不等式求解最值问题,考查计算能力,空间想象能力.
分析:设出球O1与球O2的半径,求出面积之和,利用相切关系得到半径与正方体的对角线的关系,通过基本不等式,从而得出面积的最小值.
解答:设球O1与球O2的半径分别为r1,r2,∴r1+r2+
 (r1+r2)=
(r1+r2)= .r1+r2=
.r1+r2=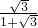 =
=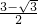 ,
,r1+r2≥2
 ,球O1与球O2的面积之和为:
,球O1与球O2的面积之和为:S=4π(r12+r22)=4π(r1+r2)2-8πr1r2≥
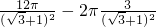
=
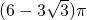 ,当且仅当r1=r2时取等号
,当且仅当r1=r2时取等号其面积最小值为
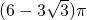 .
.故选A.
点评:本题是中档题,考查球与正方体相切关系的应用,考查基本不等式求解最值问题,考查计算能力,空间想象能力.

练习册系列答案
相关题目
两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部,且互相外切,若球O1与过点A的正方体的三个面相切,球O2与过点C1的正方体的三个面相切,则球O1和O2的表面积之和的最小值为( )
A、(6-3
| ||
B、(8-4
| ||
C、(6+3
| ||
D、(8+4
|