题目内容
空间一条直线l1与一个正四棱柱的各个面所成的角都为α,则另一条直线l2与这个正四棱柱的各条棱所成的角都为β,则下列说法正确的是________.
①此四棱柱必为正方体;
②l1与四棱柱的各边所成的角也相等;
③若四棱柱为正四棱柱,l1与这个正四棱柱的各条棱所成的角都为β,则sin2α+sin2β=1.
②③
分析:一条直线与一个正四棱柱各个面所成的角都为α,可以在正四棱柱中截取一个正方体,直线l1可以是此正方体的体对角线BH,直线l1与这个正四棱柱的各条棱所成的角也相等,最后求出体对角线与面或棱所成的角的正弦即可进行判断.
解答: 解:不妨在正四棱柱中截取一个正方体ABCD-EFGH,如图.
解:不妨在正四棱柱中截取一个正方体ABCD-EFGH,如图.
空间一条直线l1与此正四棱柱的各个面所成的角都为α,直线l1可以是此正方体的体对角线BH,直线l1与这个正四棱柱的各条棱所成的角也相等,故②正确;
但是此正四棱柱未必为正方体,故①不正确;
在图中,∠HBE=α,∠HBA=β,
且sin2α+sin2β=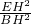 +
+ =
=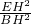 +
+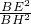 =
=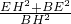 =
=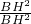 =1,故③正确.
=1,故③正确.
故答案为:②③.
点评:本题考查了直线与平面所成角的定义以及正四棱柱的概念,充分考查了转化思想的应用.
分析:一条直线与一个正四棱柱各个面所成的角都为α,可以在正四棱柱中截取一个正方体,直线l1可以是此正方体的体对角线BH,直线l1与这个正四棱柱的各条棱所成的角也相等,最后求出体对角线与面或棱所成的角的正弦即可进行判断.
解答:
 解:不妨在正四棱柱中截取一个正方体ABCD-EFGH,如图.
解:不妨在正四棱柱中截取一个正方体ABCD-EFGH,如图.空间一条直线l1与此正四棱柱的各个面所成的角都为α,直线l1可以是此正方体的体对角线BH,直线l1与这个正四棱柱的各条棱所成的角也相等,故②正确;
但是此正四棱柱未必为正方体,故①不正确;
在图中,∠HBE=α,∠HBA=β,
且sin2α+sin2β=
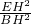 +
+ =
=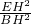 +
+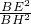 =
=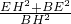 =
=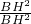 =1,故③正确.
=1,故③正确.故答案为:②③.
点评:本题考查了直线与平面所成角的定义以及正四棱柱的概念,充分考查了转化思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目