题目内容
函数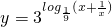 在定义域内有
在定义域内有
- A.最大值

- B.最小值

- C.最大值

- D.最小值

A
分析:先根据对数函数的性质求得x>0,进而利用均值基本不等式求得x+ 的最小值,进而根据对函数函数的单调性求得
的最小值,进而根据对函数函数的单调性求得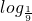 (x+
(x+ )的最大值,最后利用指数函数的单调性求得答案.
)的最大值,最后利用指数函数的单调性求得答案.
解答:要使函数有意义需x+ >0求得x>0
>0求得x>0
∴x+ ≥2
≥2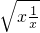 =2
=2
∴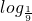 (x+
(x+ )≤
)≤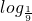 2
2
∴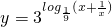 =
=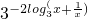 =
=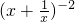 =
=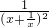 ≤
≤ ,当且仅当x=1时取等号.
,当且仅当x=1时取等号.
故选A
点评:本题主要考查了基本不等式在最值问题中的应用,指数函数和对数函数的性质.考查了基础知识的综合运用.属基础题.
分析:先根据对数函数的性质求得x>0,进而利用均值基本不等式求得x+
 的最小值,进而根据对函数函数的单调性求得
的最小值,进而根据对函数函数的单调性求得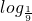 (x+
(x+ )的最大值,最后利用指数函数的单调性求得答案.
)的最大值,最后利用指数函数的单调性求得答案.解答:要使函数有意义需x+
 >0求得x>0
>0求得x>0∴x+
 ≥2
≥2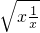 =2
=2∴
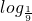 (x+
(x+ )≤
)≤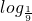 2
2∴
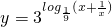 =
=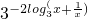 =
=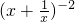 =
=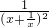 ≤
≤ ,当且仅当x=1时取等号.
,当且仅当x=1时取等号.故选A
点评:本题主要考查了基本不等式在最值问题中的应用,指数函数和对数函数的性质.考查了基础知识的综合运用.属基础题.

练习册系列答案
相关题目
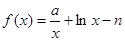 (a>0),其中
(a>0),其中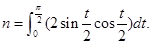 若函数
若函数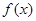 在定义域内有零点,则实数a的取值范围是 。
在定义域内有零点,则实数a的取值范围是 。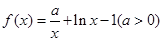 ,其中
,其中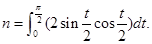 若函数
若函数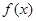 在定义域内有零点,则a的取值范围是 。
在定义域内有零点,则a的取值范围是 。