题目内容
若f(x)=1-2x,g[f(x)]= (x≠0),则g(
(x≠0),则g( )的值为
)的值为
- A.1
- B.3
- C.15
- D.30
C
分析:令f(x)=1-2x= ,可得x=
,可得x= ,由g[f(x)]=
,由g[f(x)]= 求出g(
求出g( )的值.
)的值.
解答:令f(x)=1-2x= ,可得x=
,可得x= .
.
又 g[f(x)]= (x≠0),∴g(
(x≠0),∴g( )=
)=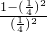 =15,
=15,
故选C.
点评:本题主要考查求函数值的方法,令f(x)=1-2x= ,求得x=
,求得x= ,代入要求的式子运算.
,代入要求的式子运算.
分析:令f(x)=1-2x=
 ,可得x=
,可得x= ,由g[f(x)]=
,由g[f(x)]= 求出g(
求出g( )的值.
)的值.解答:令f(x)=1-2x=
 ,可得x=
,可得x= .
.又 g[f(x)]=
 (x≠0),∴g(
(x≠0),∴g( )=
)=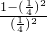 =15,
=15,故选C.
点评:本题主要考查求函数值的方法,令f(x)=1-2x=
 ,求得x=
,求得x= ,代入要求的式子运算.
,代入要求的式子运算. 
练习册系列答案
相关题目
 (x≠0),则g(
(x≠0),则g( )的值为( )
)的值为( ) (x≠0),则g(
(x≠0),则g( )的值为( )
)的值为( ) (x≠0),则g(
(x≠0),则g( )的值为( )
)的值为( )