题目内容
设点P到点(-1,0)、(1,0)距离之差为2m,到x、y轴的距离之比为2,求m的取值范围.
【答案】分析:先设点P的坐标为(x,y),然后由点P到x、y轴的距离之比为2得一元一次方程,再由点P到点(-1,0)、(1,0)距离之差为2m,满足双曲线定义,则得其标准方程,最后处理方程组通过x2求得m的取值范围.
解答:解:设点P的坐标为(x,y),依题设得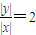 ,即y=±2x,x≠0
,即y=±2x,x≠0
因此,点P(x,y)、M(-1,0)、N(1,0)三点不共线,得||PM|-|PN||<|MN|=2
∵||PM|-|PN||=2|m|>0
∴0<|m|<1
因此,点P在以M、N为焦点,实轴长为2|m|的双曲线上,故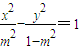 .
.
将y=±2x代入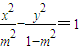 ,并解得
,并解得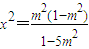 ≥0,
≥0,
因为1-m2>0,所以1-5m2>0,
解得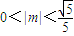 ,
,
即m的取值范围为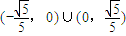 .
.
点评:本题主要考查双曲线定义及代数运算能力.
解答:解:设点P的坐标为(x,y),依题设得
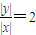 ,即y=±2x,x≠0
,即y=±2x,x≠0因此,点P(x,y)、M(-1,0)、N(1,0)三点不共线,得||PM|-|PN||<|MN|=2
∵||PM|-|PN||=2|m|>0
∴0<|m|<1
因此,点P在以M、N为焦点,实轴长为2|m|的双曲线上,故
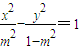 .
.将y=±2x代入
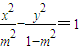 ,并解得
,并解得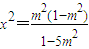 ≥0,
≥0,因为1-m2>0,所以1-5m2>0,
解得
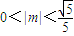 ,
,即m的取值范围为
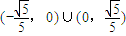 .
.点评:本题主要考查双曲线定义及代数运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目