题目内容
2012年1月1日,某地物价部门对该地的5家商场的某商品一天的销售量及其价格进行调查,5家商场该商品的售价x元和销售量y件之间的一组数据如表所示,由散点图可知,销售量y与价格x之间有较好的线性相关关系,其线性回归直线方程是
=-3.2x+a,则a=
| ? |
| y |
40
40
.| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | 10 | 8 | 6 | 5 |
分析:先计算平均数,再利用线性回归直线方程恒过样本中心点,即可得到结论.
解答:解:由题意,
=
=10,
=
=8
∵线性回归直线方程是
=-3.2x+a,
∴8=-3.2×10+a
∴a=40
故答案为:40
. |
| x |
| 9+9.5+10+10.5+11 |
| 5 |
. |
| y |
| 11+10+8+6+5 |
| 5 |
∵线性回归直线方程是
| ? |
| y |
∴8=-3.2×10+a
∴a=40
故答案为:40
点评:本题考查线性回归方程,利用线性回归直线方程恒过样本中心点是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
2012年1月1日,某地物价部门对该地的5家商场的某商品一天的销售量及其价格进行调查,5家商场该商品的售价x元和销售量y件之间的一组数据如表所示,由散点图可知,销售量y与价格x之间有较好的线性相关关系,其线性回归直线方程是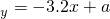 ,则a=________.
,则a=________.
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | 10 | 8 | 6 | 5 |
2012年1月1日,某地物价部门对该地的5家商场的某商品一天的销售量及其价格进行调查,5家商场该商品的售价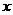 元和销售量
元和销售量 件之间的一组数据如下表所示,由散点图可知,销售量
件之间的一组数据如下表所示,由散点图可知,销售量 与价格
与价格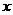 之间有较好的线性相关关系,其线性回归直线方程是
之间有较好的线性相关关系,其线性回归直线方程是 ,则
,则 .
.
|
价格x(元) |
9 |
9.5 |
10 |
10.5 |
11 |
|
销售量y(件) |
11 |
10 |
8 |
6 |
5 |
 元和销售量
元和销售量 件之间的一组数据如下表所示,由散点图可知,销售量
件之间的一组数据如下表所示,由散点图可知,销售量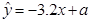 ,则
,则 .
.